この記事で扱っていること
- ビンゴをシミュレートする方法
を紹介しています。
注意:すべてのエラーを確認しているわけではないので、記事の内容を実装する際には自己責任でお願いします。また、エラー配線は適当な部分があるので適宜修正してください。
ビンゴは、5×5のマスに1から75の数字が当てはめられたカードがプレイヤーに配られ、一つずつランダムで選ばれる数字が各プレイヤーのカードに記載されているならその番号に印をつけ、選ばれる数字が増えて印がつく数字も増え最終的に印が縦か横か斜め方向に連続5個つけば上がり、というルールが一般的かと思います。
5×5のマスのど真ん中はFree枠として最初から印をつけておくことができ、これを含めて連続5個揃った形でも上がりですね。
あるとき、ふと、「ビンゴって何回数字が選ばれたら上がれるのだろう」という疑問が浮かびました。
Free枠含めた上がりを考慮すると、最小では4つの数字が選ばれて上がりになるパターンはあり得ると思いますが、確率的には相当低いはずです。
数学的に計算をすればわかると思いますが、なんだか複雑そう・・・そんなわけでこれをLabVIEWで確かめてみます。
同じプログラムを別の視点で使ってみた動画も作ったのでよければご覧ください。
どんな結果になるか
まずは、ビンゴゲームを模擬するところから始めます。
フロントパネルには、ビンゴの盤面と、印がついた位置を表示するためのブール配列、ランダムで選ばれた数とビンゴまでにかかった回数を示す数値表示器、そしてビンゴになったら光るLEDを配置しています。
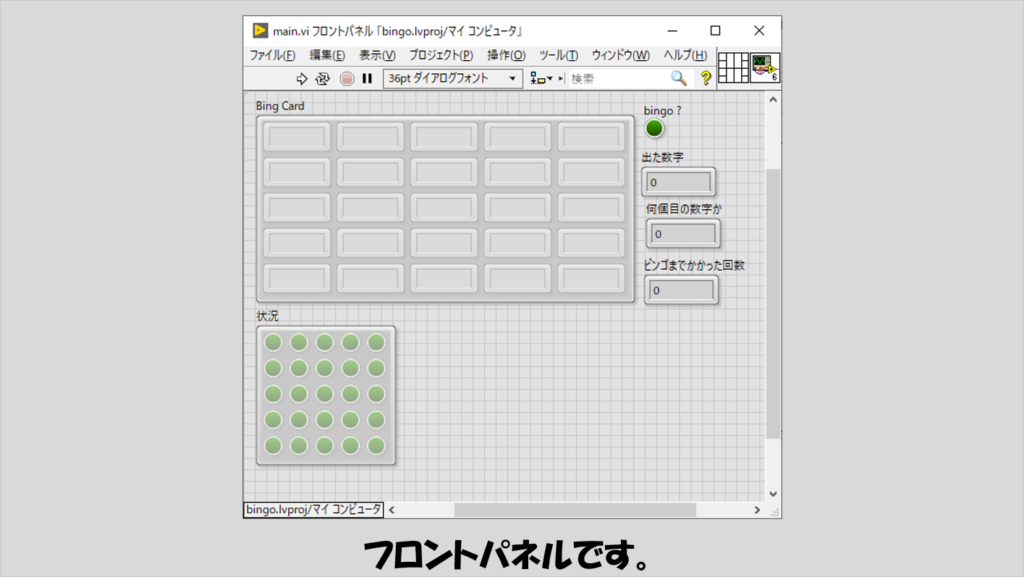
プログラムを実行すると、盤面が作成され次々と数字が選ばれていき、ビンゴカードにある数字が選ばれた場合には対応するブール配列に印が付き、縦横斜めいずれかで揃ったらプログラムが止まります。
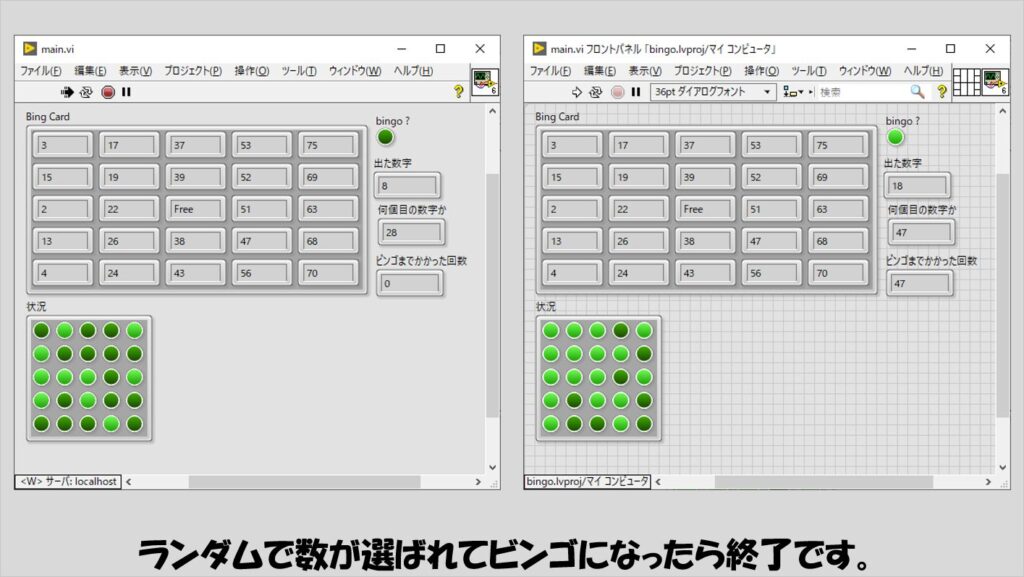
プログラムの構造
プログラムでは最初に盤面を作成し、その後にWhileループに入ってビンゴが成立するまでプログラムが回り続けます。

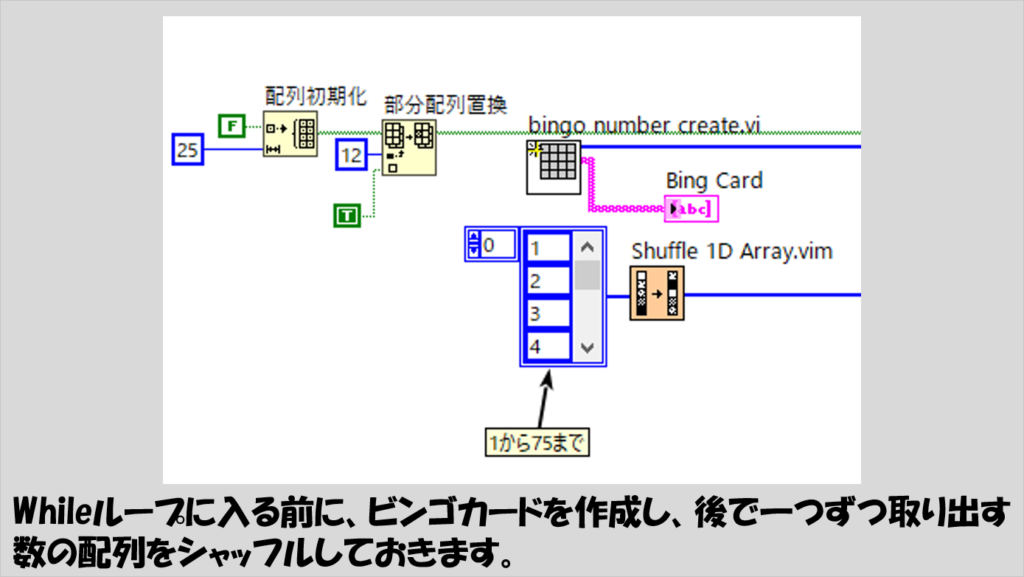
Whileループに入る前にブールの配列を作っておきます。
ただ、ビンゴ判定の仕方の都合上、ここで用意しているのは2次元ではなく1次元配列になっています。
5×5の盤面を1次元配列としてみなしたとき、「真ん中」は要素番号が12の場所になるので、この1次元ブール配列の要素12だけ先にTrueにしています。
また、Whileループの中で「取り出す」数もループの外で用意しておきます。
配列定数には1~75までの数があり、これをランダムでシャッフルしています。
つまりループに入る時点でビンゴカードと取り出す数の順番も決定している状態となります。
Bingo number create.viではビンゴの盤面を作っていきます。
(恐らく)一般的なビンゴでは、各列(よくカードでそれぞれの列に対して「B」「I」「N」「G」「O」などと表記されていると思います)に対して、「B」列は1から15までのいずれか5個、「I」列は16から30までのいずれか5個、などと決まっていると思います。
これを表すため、それぞれの列ごとにランダムシャッフルした配列を作りだして毎回5個の要素を部分配列関数で取り出し、これをForループから取り出すときに自動指標付け有効の状態でとりだしています。
ただし、Forループの自動指標付け有効で取り出した場合、各ループの配列の結果が列方向に追加されていくことになるため、「B」「I」「N」「G」「O」という列の向きに各ループでの結果を表示させるためには転置する必要があります。
またこの盤面の表示を数値ではなく文字列(の2次元配列)としているのは、真ん中の部分をFreeと表記するためです。
bingo dataの表示器としては、後の処理を考えると2次元配列より1次元配列の方が扱いやすいため配列次元変更で1次元配列としています。

メインviの方でWhileループに入ったら、取り出す数の配列から要素1つずつを取り出しています。
これが「出た数字」となり、detect hit number.viに渡されます。
detect hit number.viでは、ビンゴカードとしての1次元配列であるcard data inの中から、「出た数字」の数があるかどうかを1D配列検索で調べ、ブール配列を更新します。
「出た数字」があったらTrueに置換、ない場合でもFalseに置換、と考えればケースストラクチャは必要ありません。
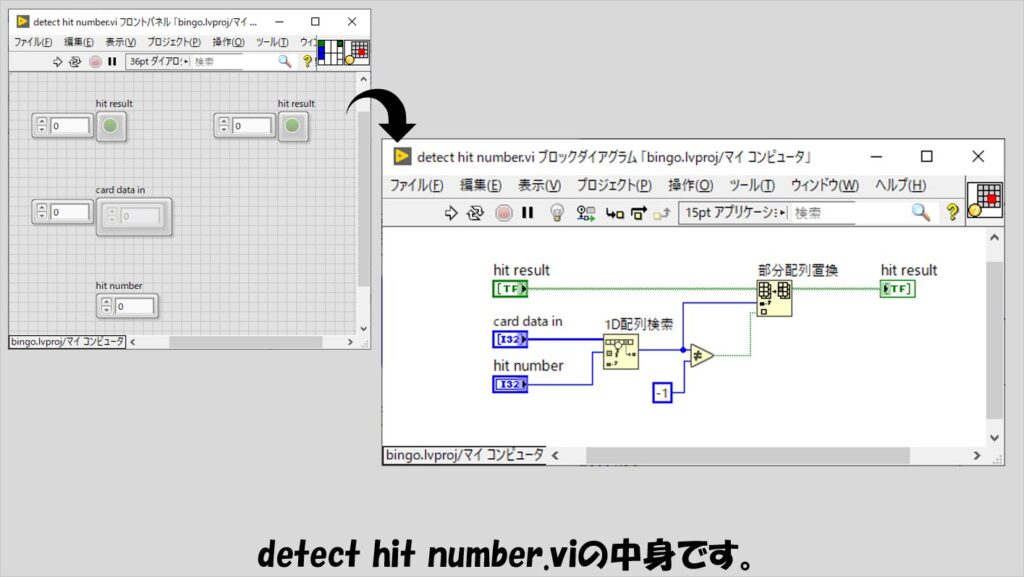
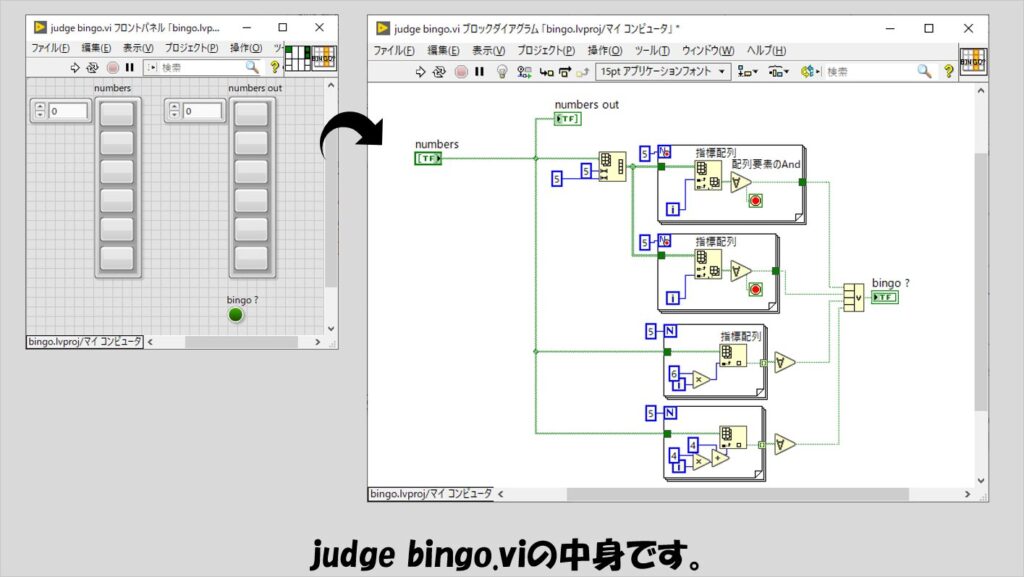
detect hit number.viのあとはビンゴであるかを判定するjudge bingo.viに進みます。
judge bingo.viでは縦、横、斜め(左上から右下、もしくは右上から左下)に対してブール配列の要素を調べて全てがTrueであるかを調べます。
斜め方向を調べるのは一見難しそうですが、5×5の25マスのビンゴを1D配列にした場合、左上から右下にかけての斜めのマスは、配列要素番号でいう0、6、12、18、24で固定されていたり、右上から左下にかけての斜めのマスも4、8、12、16、20で固定されているのでこれらの要素を調べるだけです。
何回目でビンゴになる確率が一番高いのか
では、ビンゴゲーム1回分のシミュレーションを行うプログラムができたところで、これを何度も繰り返し、何個の数が出たらビンゴになるかの統計をとってみます。
Forループを使用して以下のようにプログラムを書きます。
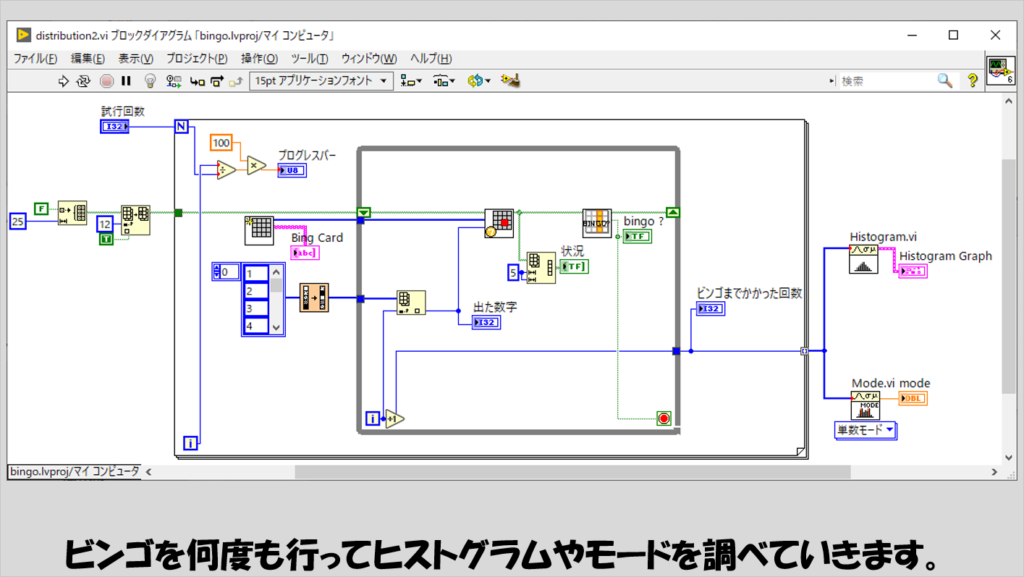
試しに1000回、10000回、100000回行った結果を紹介します。
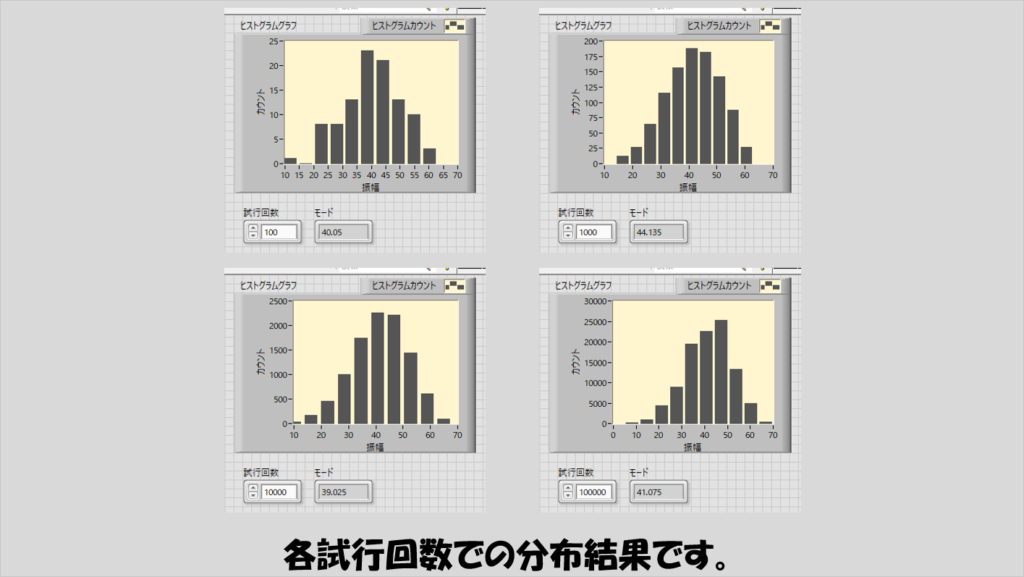
これが本当に期待される結果なのか、というのは何か別の参考データがないとわからないですが、ネットで検索する限り、40回前後数字が出たらビンゴになる確率が最も高いらしいので、今回のシミュレーション結果とも一致していそうです。
本記事では、LabVIEWでビンゴをシミュレートする方法を紹介しました。
こういった題材は数学的な解析も大切とはいえ、プログラミングで実際に試して結果を知るようなアプローチも面白いと思います。
ハードウェア制御だけではない、演算処理にもLabVIEWが活用できるという一例として参考になればうれしいです。
ここまで読んでいただきありがとうございました。

コメント