この記事では、LabVIEWによって数学の確率分野の計算をシミュレーションする題材として、モンテカルロ法により円周率の近似値を求める様子をLabVIEWで表現するプログラムを紹介しています。
モンテカルロ法とは
モンテカルロ法は、乱数を大量に用いて複雑な問題の近似的な解をコンピュータによるシミュレーションによって力業で得るための手法になります(数学に詳しい人からしてみると怒られてしまうような雑な説明かもしれませんが)。
実は以前書いたビュフォンの針によって円周率を求めるというテーマも、モンテカルロ法の一例と言えます。
ただ、ビュフォンの針は設定を理解すること自体は難しくないものの、ここから円周率を求めるという過程の数学的な背景に三角関数が使われているなど、数学が苦手な方にとっては天敵(?)がいるため、試しにくかったかもしれません。
今回は、もう少し数学的な背景が易しいテーマとして円周率の近似解を求めていきます。
考えるのは正方形とその正方形に内側から接する(内接する)円です。
そして、正方形の内部のどこかにランダムでN個の点を打ってそのうち円の内側に打たれた点の数をn個としたとき、
(正方形の面積):(円の面積)=N:n
という関係で表せることから、円周率を求めていきます。
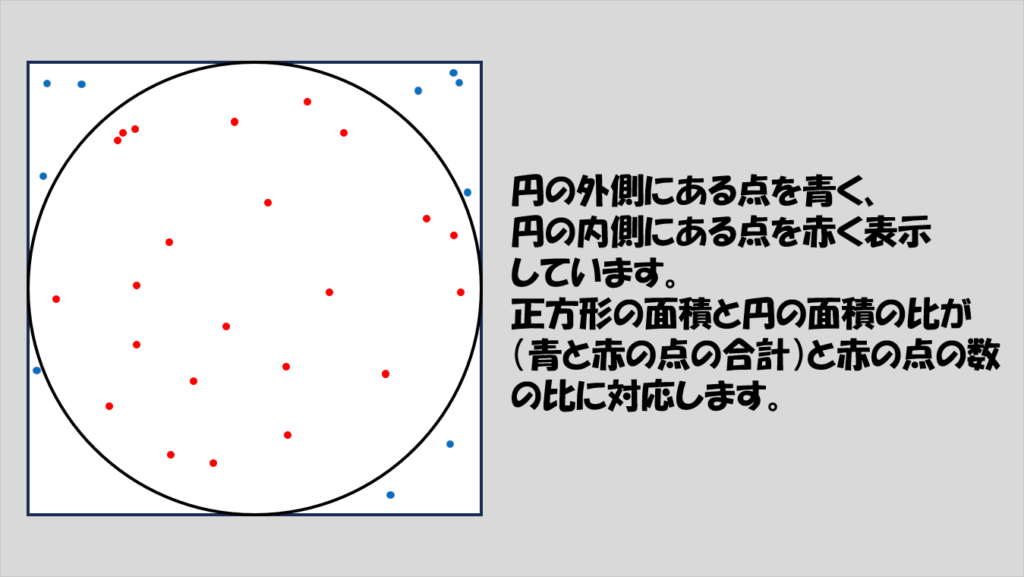
どうやってこの式が出てくるかについての背景は記事後半で紹介しています(厳密さよりも直感を重視した説明になっているのでご注意ください)。
どのような結果になるか
フロントパネルには、試行回数を指定するための数値制御器、プログラム実行時に何点打ったかを示す数値表示器、あとはシミュレーションの過程を表示するためのピクチャ表示器の大きさを指定するための制御器と、求めた円周率を表示する表示器を置いています。
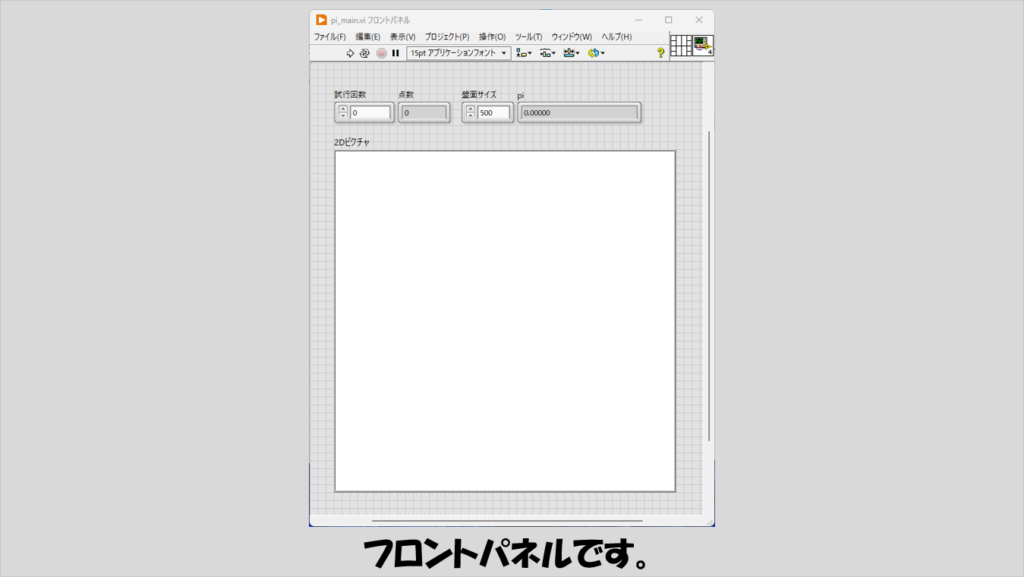
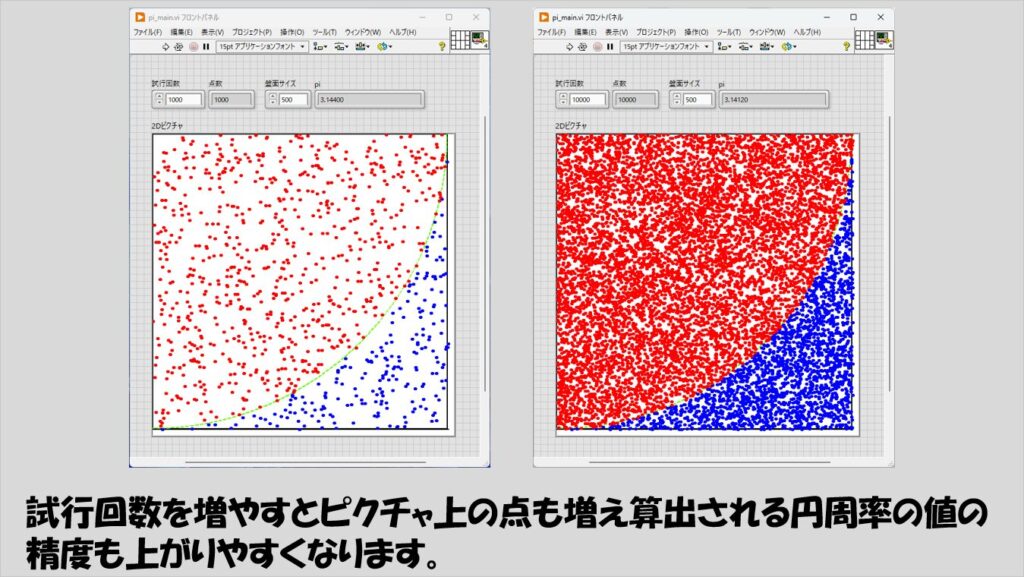
プログラムを実行すると、円(ここでは円全体ではなく4分の1円としています)の内外に指定した数の点がランダムで打たれ、先ほど紹介したNとnの関係から円周率を算出できます。
基本的には、点の数を指定する、「試行回数」の部分の値を大きくするほど、真の円周率の値に近づきやすくなっていることがわかります。
プログラムの構造
ではプログラムの構造を紹介します。
ビュフォンの針と比べるとだいぶシンプルで、計算をするだけならもっと小さいプログラムになりますが、ピクチャ表示器にシミュレーションの過程を表示するためにピクチャを操作する関数を使用する必要があります。
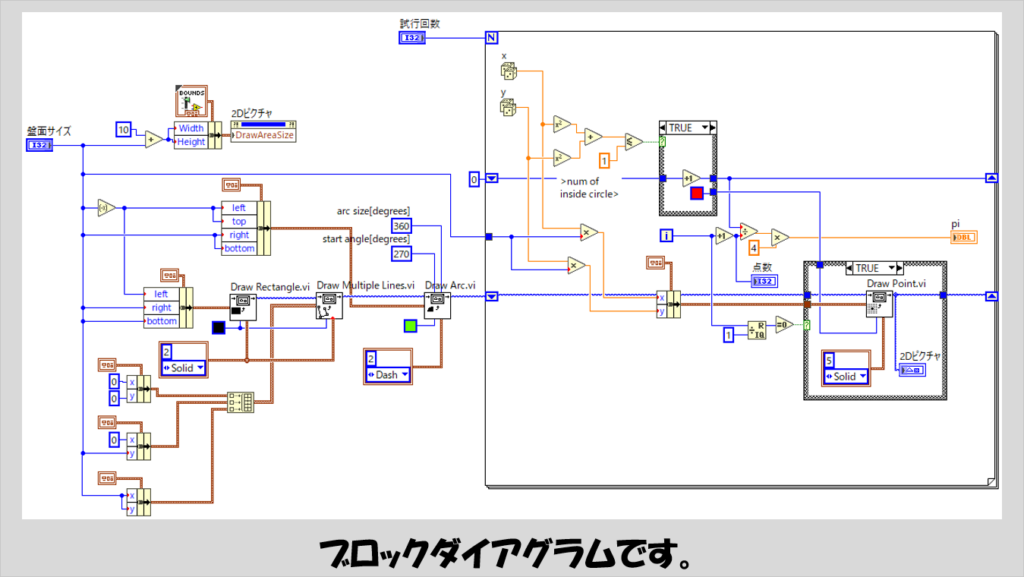
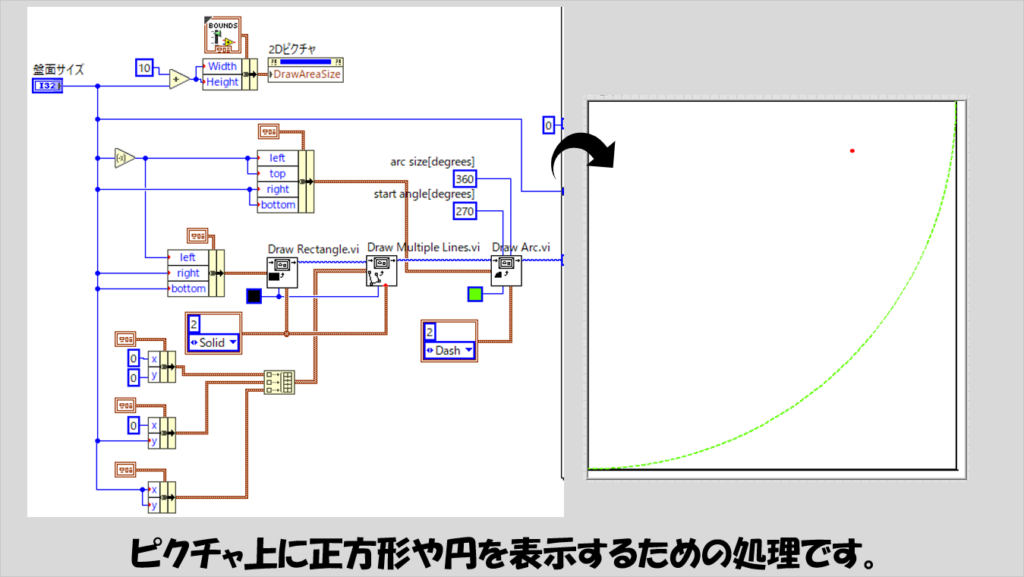
Forループに入る前は、ピクチャ上に正方形や円を表示するための処理を行っています。
ピクチャ上に図形を書くときには座標を指定する機会が多いですが、ピクチャ表示器の場合には座標原点が左上にあるので、いわゆるxy座標として考えた時、xは右に行くほど大きくなり、yは上ではなく下に行くほど大きくなることに注意します。
Forループの中では、乱数を用いてランダムに打つ点の座標を決めています。
円の内側にくるかどうか、は打った点のx、y座標の値をそれぞれ2乗しこれらの和が1より小さいかどうかで判断できます(円の半径を1とした場合)。
1より小さい、円の内側になった場合には、内側に来た点の数をカウントを1増やし、外側になった場合にはカウントは増やしません。
このカウントを、点の数で割って4を掛けることで円周率を算出しています。
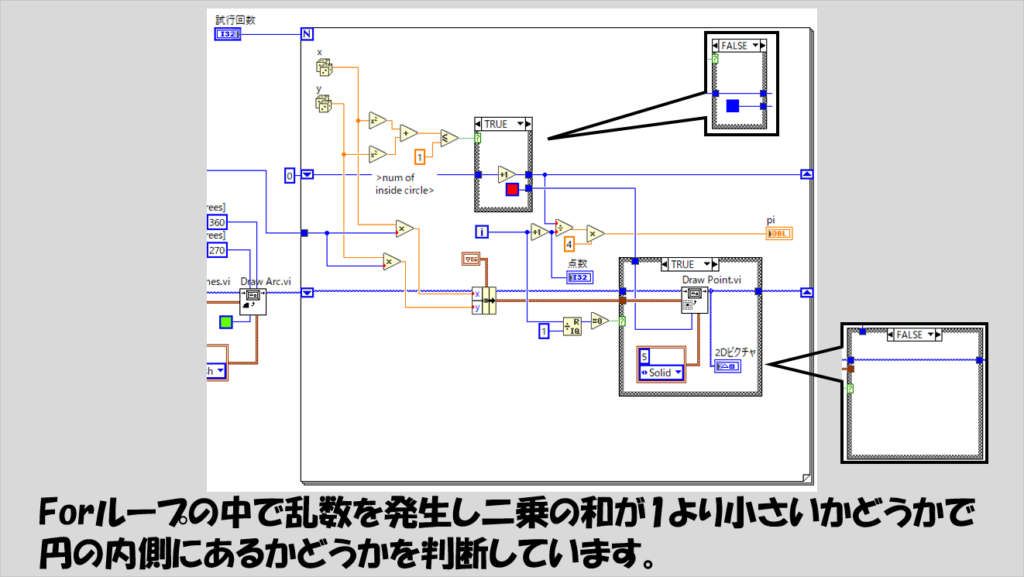
なお、Forループの中の右下にあるケースストラクチャは、すべての点をピクチャに表示するわけではない場合に点の数を調整する処理のために使用しています。
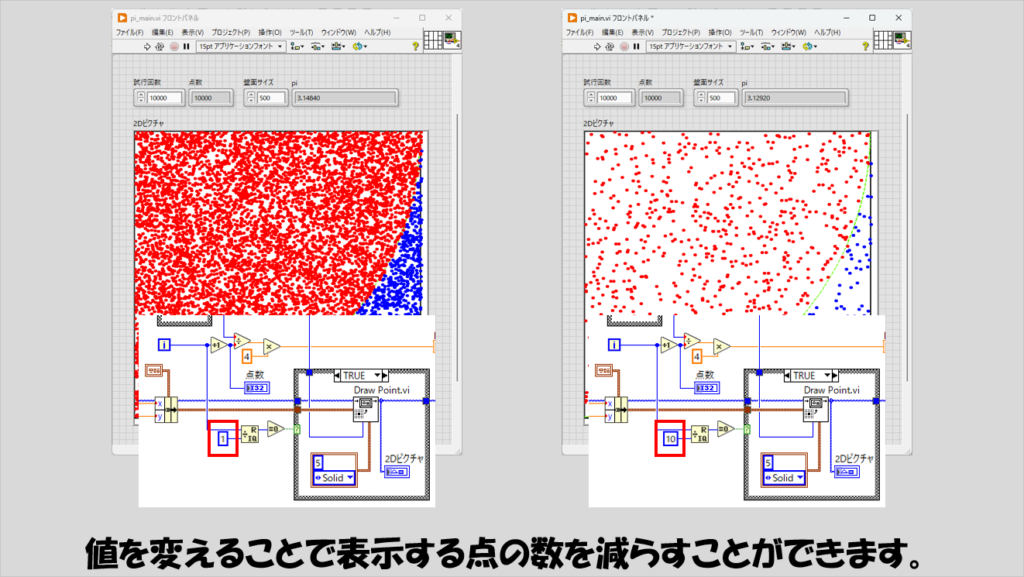
Forループの反復端子の値を任意の数で割った余りが0になったときにピクチャ表示させることで点の数を調整することができます。
例えば、反復端子の値を1で割った場合にはすべての点を、10で割った場合には、試行回数として指定した点の10分の1の数の点をピクチャ上に表示することになります。
数学的背景
最後に、どうして円周率が求められるかという数学的な背景を紹介していきます。
ネットで「モンテカルロ法」と調べたらいくらでも情報は出てきますが、ここでは数学的な厳密さより直感的なイメージ重視で説明したいと思います。
まずは正方形に内接する円を考えます。

そしてこの正方形の中のどこかにランダムで1つ点を打つとします。
この正方形の中のどこかに打つ、ということなので、もしかしたら円の内側に打たれるかもしれないですし、円の外側(で正方形の内側)に打たれるかもしれません。
とにかく、円の内側外側であるかどうかは気にせず、ランダムな位置に1点打ちます。

ここで、打った点が円の内側に来る確率を求めてみます。
どうやってそんなものを求めるかについてですが、ここではイメージで説明します。
いったん、正方形の内側の円について、「内接する」という条件を取り除きます。
そして、円の中心はそのままに、自由に円の大きさを変えられたとします。
このとき、円の内側に点がくる確率を最大にするにはどうすればいいかというと、円を一番大きくすればいいはずです。
円が小さいほど、「円の内側にランダムな1点が打たれる」確率が低くなる(言い方を変えると円が大きいほど確率が高くなる)ことは直感的にわかるかと思います。
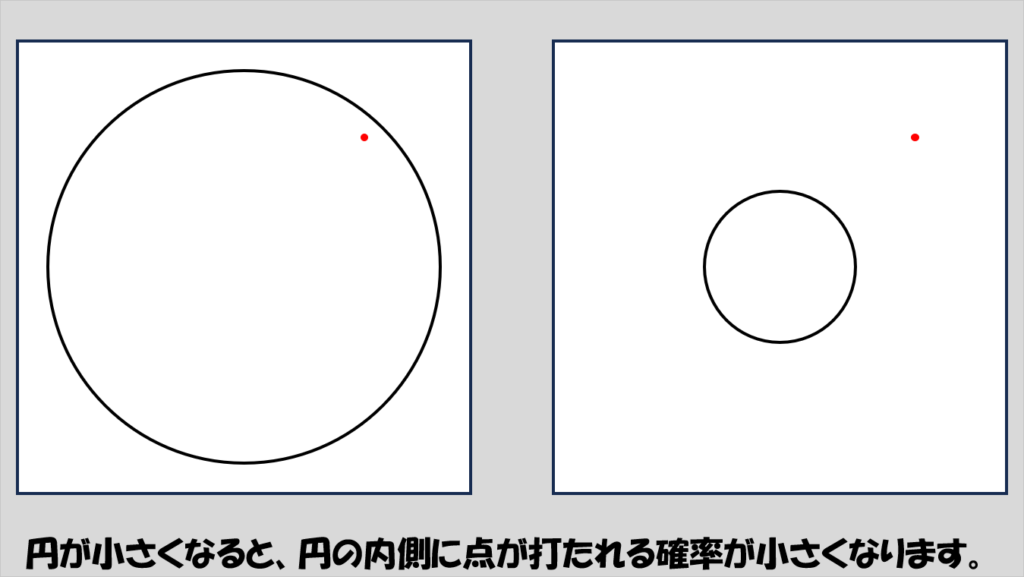
ここで言っている円の大きい、小さいとはつまり円の面積が大きい、小さい、という話です。
つまり、「面積」と「確率」は比例する(面積が大きくなるとその分確率も大きくなる)、ということになります。
では、円が正方形に内接しているという条件に戻り、改めて円の内側に点が打たれる確率を考えてみます。
確率とは、起こりうるすべての現象の数に対して、対象とする(確率を調べたい)現象の数の比で表せます。
今回の例でいうと、起こりうるすべての現象とは、正方形の内部に点が打たれている状態を指します。
一方で、対象とする現象とは、円の内部に点が打たれている状態です。

これを先ほどの面積の話に置き換えると、
- 起こりうるすべての現象の数は正方形の面積に比例する
- 対象とする現象の数は円の面積に比例する
と言えます。
もし1つしか点が打たれていない場合には、起こりうるすべての現象の数は1です。
必ず正方形の中に点があるから、ですね。
で、円の内部に点が打たれている状態の数は0か1で、例えば円の内部に点があったとしたら1です。
計算を簡単にするために、円の半径を1としたとき、正方形の面積は4、円の面積はπとなります。
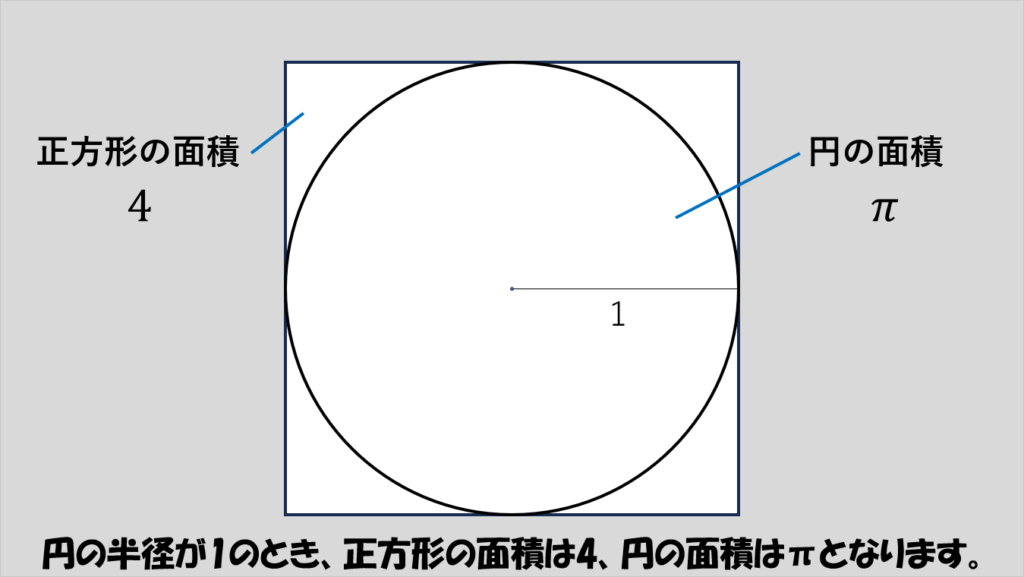
これらから、
4:π=1:1
という式を導け、π=4となります。
・・・もちろんこれはπの値として間違っているため、試行回数を増やす、つまり、もっと多くの点を正方形の内側に打っていきます。
例えば、正方形の内側に合計で100点を打ち、そのうち円の内側に80点入ったとします。
すると、
4:π=100:80
という式となり、このときπ=3.2となります。
さっきよりは円周率として知られている値、3.14159・・・に近づきました。
これを、もっと多くの点を使ってやることで近似値を求めていくのですが、膨大な数の点をランダムに生成していくという作業でプログラミングの出番となり、今回紹介したプログラムに至ります。
本記事では、モンテカルロ法で円周率を求めるシミュレーションの実装例を紹介しました。
何か特定の処理、作業を膨大な回数行うことで近似解を求めるという手法は円周率の近似だけでなくいろいろな分野で応用できると思います。
プログラミングが苦手な方でも扱いやすいLabVIEWを使ってぜひ様々な題材でシミュレーションにチャレンジしてみてください。
ここまで読んでいただきありがとうございました。


コメント