この記事では、LabVIEWによって数学の確率分野の計算をシミュレーションする題材として、ビュフォンの針を実際にLabVIEWで再現して試すプログラムを紹介しています。
これは実際にプログラムを実行している様子を見るのも面白いで、別途動画で紹介しています。
よろしければご覧ください。
ビュフォンの針とは
まず本記事で取り上げているビュフォンの針とはそもそも何なのかについてですが、これはとてもざっくり言えば、ある実験を繰り返すことによって円周率の近似値を求める方法になります。
(以降、厳密な話はしません、専門の人が見たら間違っている部分もあるかと思いますが、ご了承ください)
ある実験というのは、紙とペン、そして無数の「針」を用意することでできます。
紙に、等間隔で線を引いて床に置いておきます。
このとき、等間隔である線の間隔の長さをdとします。
そして、紙の上から無数の針を落としていきます。
このとき、針は無造作に紙の上に落下していきますが、紙に書かれた線と交わるものもあれば交わらないものもあるはずです。

とても極端な話をしてしまうと、例えば紙の上の線分が無限の長さを持っていて針も無限の長さを持っている場合には、紙の上の線と完全に平行な向きで針が落ちているのではない限りどこかで交わってしまうため、ここでは針の長さに制限を付けることにします。
また、後の計算のしやすさの都合から、針の長さlは線の間隔dの半分だとします(つまり2l = dという関係)。
このとき、「紙の上の線と交わっている針」は個数を数えればわかる量になりますが、これと、全針の割合から円周率の近似値が求まります。
ただし、何となく想像してもらったらわかると思いますが、針を例えば100個程度落としたところで、あまり円周率に近くはなりません。
理屈ではこうだろう、というものでも数を多くしないと確かめられないことであれば・・・プログラム的にシミュレートしてみます。
なお、次の章ではプログラムの中身を紹介します。
実装しているのは上で説明した内容を数学的に表現したものですが、数学的な背景については記事後半のおまけとして紹介しています。
プログラムの構造
ではプログラムの構造を紹介します。
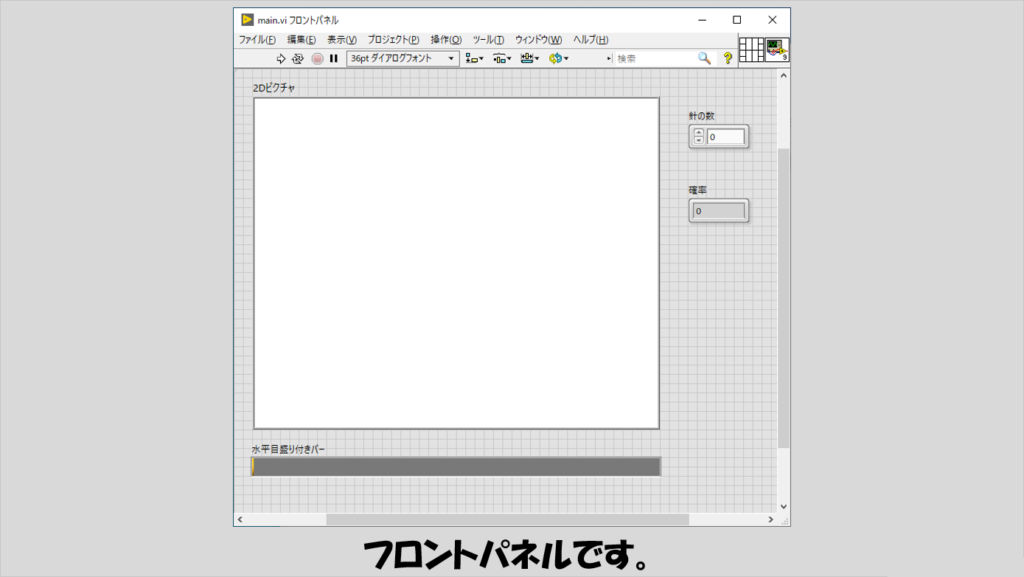
フロントパネルには、「針」が無造作に置かれていく様子を示すためのピクチャを用意します。
また、プログラムが終わるまでの時間を表したプログレスバーも配置しておきます。
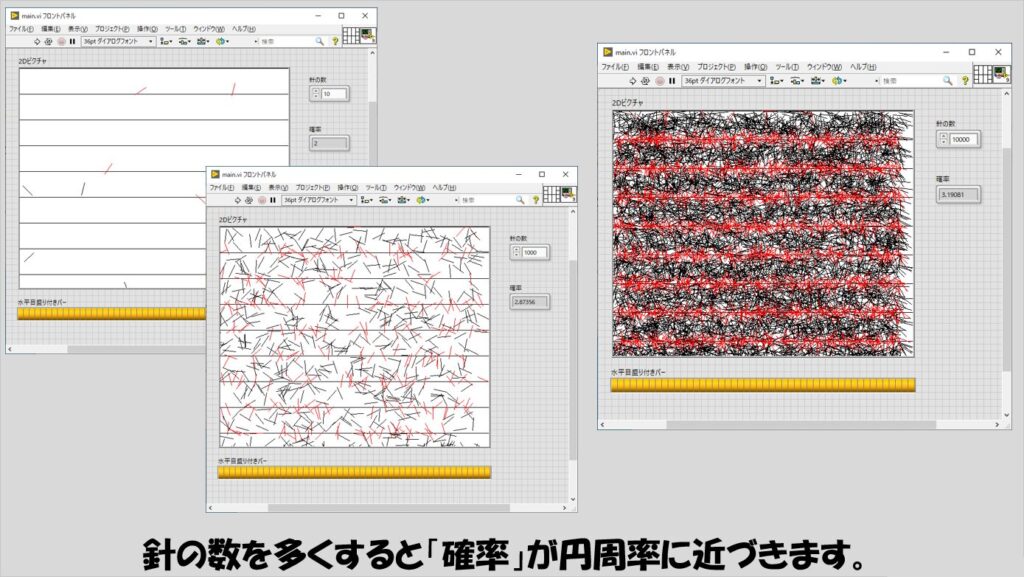
プログラムを実行すると、ピクチャ上に横線が表れ、針も表示されます。
横線をまたいだ針は赤く表示され、またいでいない針は黒く表示されるようにしあとはひたすら針の数が指定した数に達するのを待ちます。
最終的に針全体に対しての横線をまたいだ針の割合を円周率とみなしています。
ちなみに今回試したところ以下の図のような結果となり円周率は「3.19」程度となっています。
もちろん毎回やる毎にこの結果は異なります。
ブロックダイアグラムはシンプルで、横線を表すパートと、針を表現するパートに分かれています。
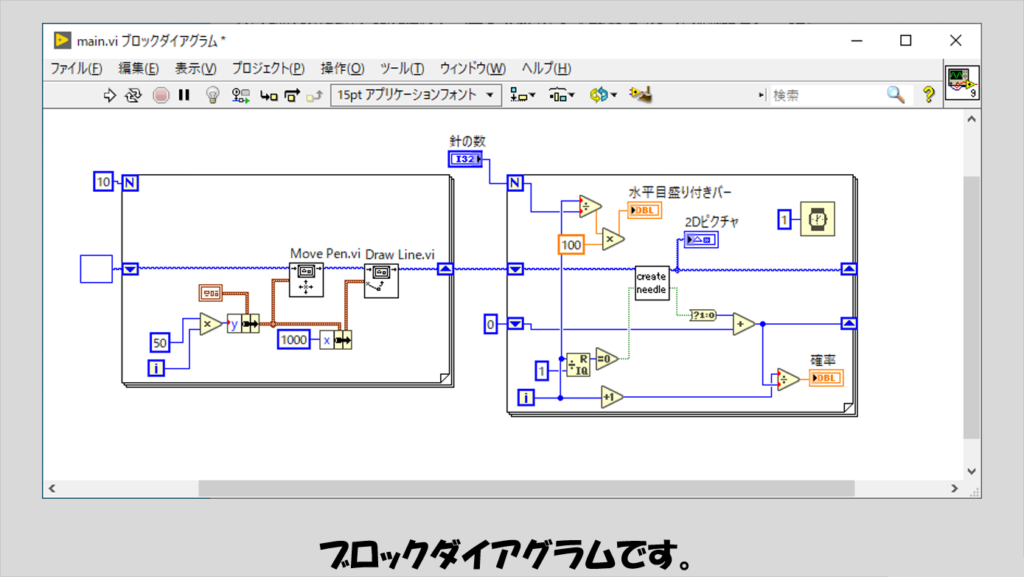
横線を表すパートはピクチャ関数のペン移動とライン描画を交互に使っています。
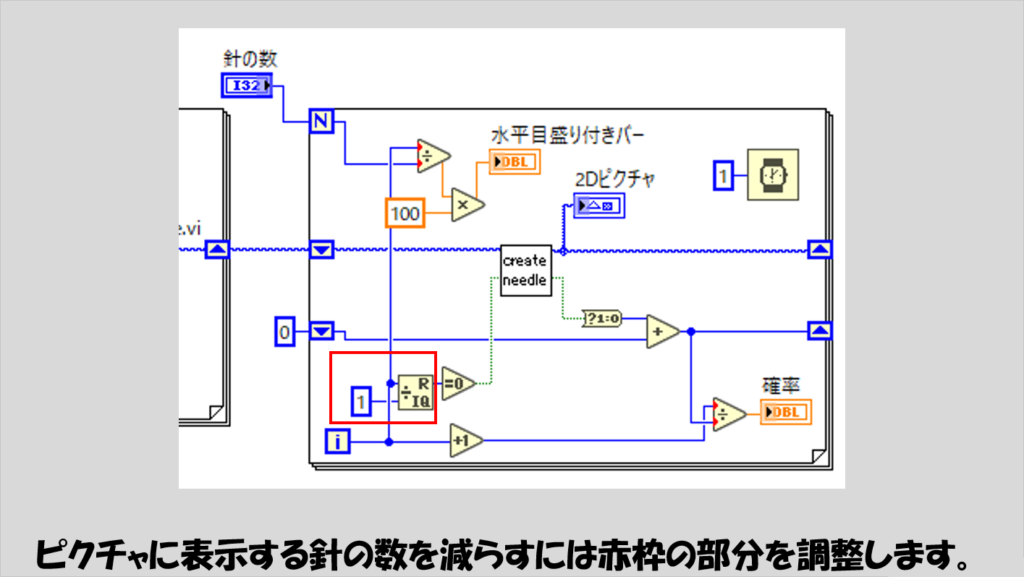
直線の間隔を変えるには、下の図の赤枠で示した値を変更します。
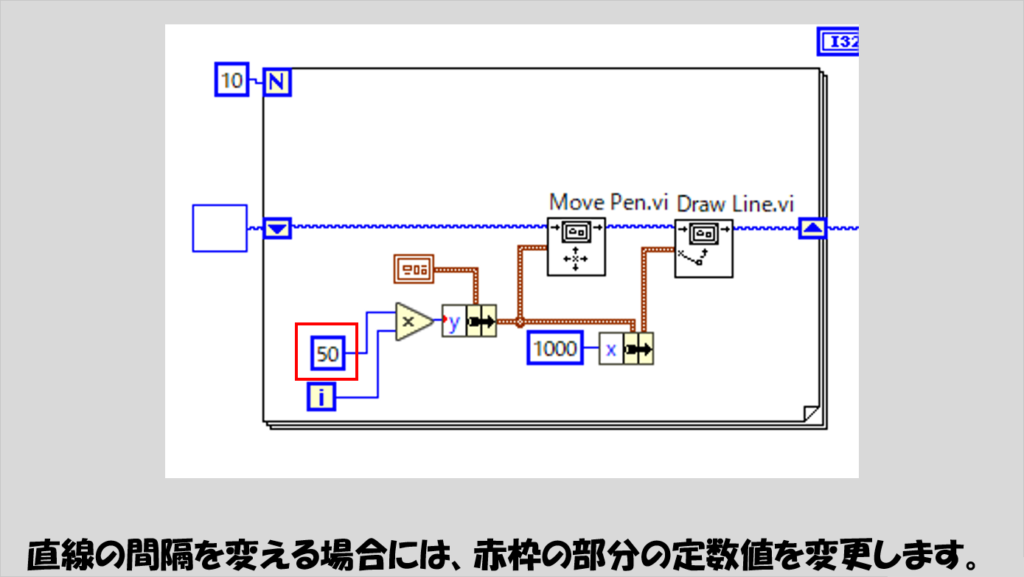
次に針を表示する方のプログラムですが、こちらについては針の表現はサブVIの中で行っています。
今回のプログラムでは、針の数を大きくするとそれだけピクチャに表示する必要があり処理負荷が大きくなります。
そこで最終的な計算上では全ての針を扱うものの、ピクチャ上に表すのは、その何分の一か、にするために、下の図の赤枠のような仕組みを設けています。
Forループの反復端子の値をある数で割ってその余りが0になったらTrueとなるブール値をサブVIに渡します。
この数(下の図では「1」ですが)は「何分の一」の「何分」に相当するので、例えば数を「2」にすると、ピクチャに表す針の数は指定した針全体の2分の一となります。
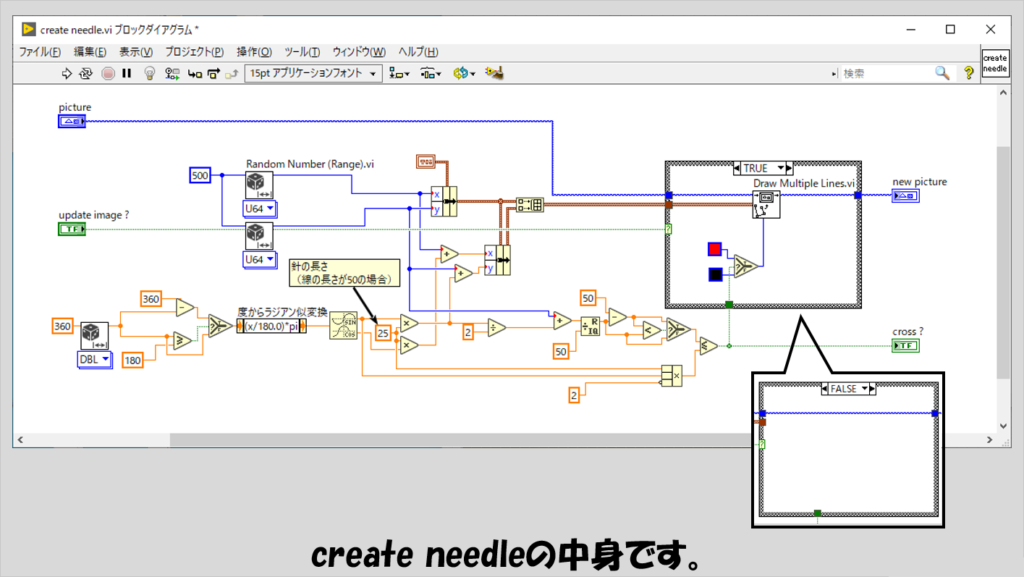
サブVIの中身は以下のようにしています。
針をランダムで生成するために乱数を使用し、その角度をラジアンに変換、これに三角関数のサイン、コサインに変換する関数を使用して針を表現しています。
計算をすることで針が線をまたいだかを判定し、その結果をcrossというブールでメインVIに渡して、メインVIではこれが何回Trueになったかを数えます。
数学的背景
ここでは、上記プログラムで演算している数学的な内容について補足的に紹介していきます。
まず、冒頭でのビュフォンの針の紹介でも書きましたが、紙の上の線の間隔dと針の長さlにはl = 2dという関係があるとします。
(これは計算の都合上の話で、実際はこの関係がなくてもいいのですが)
数学的に、針が紙の上の線と交わるというのがどういう状況かということを調べる必要があります。
そこで、紙上のある場所に落下した針に対して、その針の真ん中の座標をP(X,Y)とします。
紙の上の線は、X軸と並行に引かれているとして、座標Pから線に垂直に線を引いたときにもっとも近くで交わる線があるはずで、その線からの距離をhとします。
また、針はX軸(線と並行)に対してある角度 をなしておかれているとしたときに、針の先端までの長さは(l/2)sin と表せます。
針と線が交わるのは、hと(l/2)sinθ に対して、h≤り立つときであるのが下の図から分かると思います。
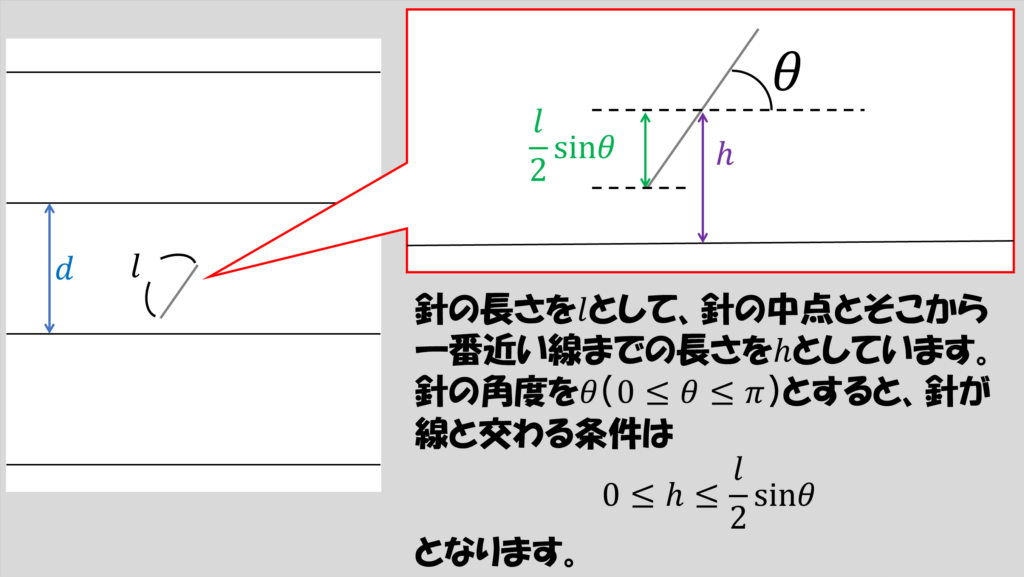
ただし、前提条件からhはd/2より大きくなることはなく(なぜならd/2より大きくなった時点で別の線に対してより近くなるため、より小さいh’が存在することになるから)、また、 θは180度(π )を超えることもありません。
針は線に対して様々な位置、角度で存在しうるわけで、究極的には全てのhやθとして取りうる値になります。
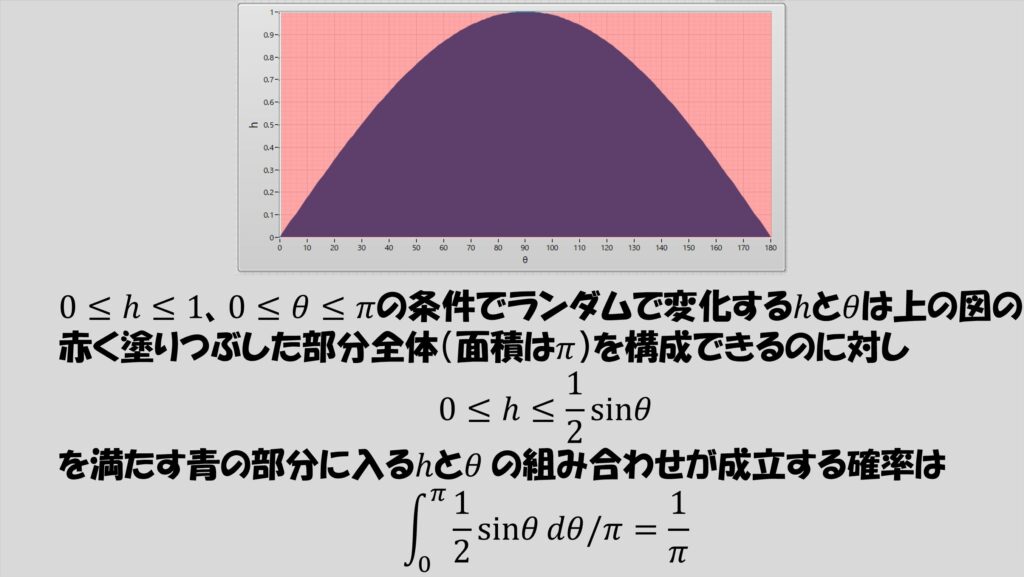
その中で、針が直線と交わる条件、h≤(l/2)sinθを満たすときのhとθの組み合わせで形成できる部分の面積は、h=(1/2)sinθの線の下の部分の面積となるので以下の図の青で示した部分であり、これは面積が1となります(l=1を代入済み)。
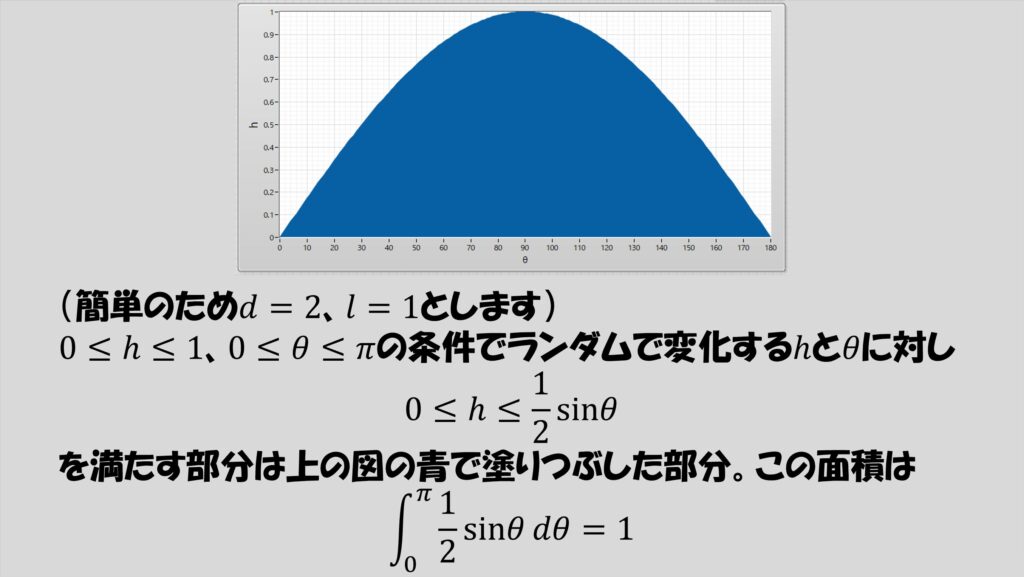
当然、線と交わらない針もあるはずなので、線に交わっているかどうかに関係なくhとθがとりうる値すべての範囲で形成される部分の面積は下の図の赤で示した部分であり、これは面積がπになっているはずです。
つまり、全ての針に対して、線と交わる針の割合は1/πと求まります。
この考えをプログラム中の演算処理に落とし込んだのが上で紹介したプログラムになります。
針の長さと線の間隔が都合よすぎないか?と思った方もいるかもしれませんが、この前提が無くてもビュフォンの針の考え方は適用できます(気になる方は調べてみてください)。
本記事では、LabVIEWでビュフォンの針をシミュレートする方法を紹介しました。
現実世界で針を何百何千何万おとして実験するのは文字通り「非現実的」となりますがプログラムの上では(時間があれば)いくらでも試せて、結果的に円とは全然関係ない実験なのに円周率が求まるという変わった結果を得ることができます。
LabVIEWも他のプログラミング言語同様こうしたシミュレーションにも使えるという一例として参考になればうれしいです。
ここまで読んでいただきありがとうございました。



コメント