ライフゲームを作る

この記事で扱っていること

• ライフゲームを作る方法

を紹介しています。

注意：すべてのエラーを確認しているわけではないので、記事の内容を実装する際には自己責任でお願いします。また、エラー配線は適当な部分があるので適宜修正してください。

ライフゲームとは、直訳すれば人生ゲームですが、ルーレットを回してコマを進めながら人生を疑似体験するあのパーティゲームを扱うわけではありません。

（区別のため、今回紹介するライフゲームはConway’s Game of Lifeと呼ばれます）

シミュレーションの一種で、生命の誕生から死の様子を世代ごとに観察していくもので、ゲームと名がついている割に基本的にユーザーはプログラムの最初に初期条件を決める以外に操作することはありません。

ただ、初期条件が違っただけでその後の経過が大きく変わり、その変化の様子は見ていて結構楽しめます。

記事後半では、特徴的なパターンの例を紹介していきます。

どんな結果になるか

今回は、ブールの表示器でライフゲームのマスを表現していきます。

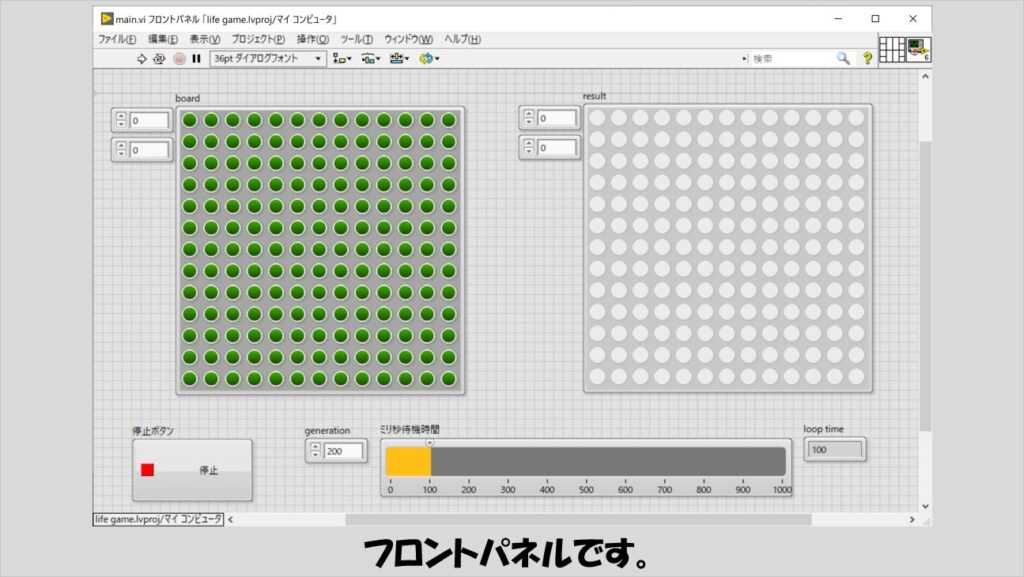
マス一つが一つの生命と考えて、あるマスに対して周りを取り囲む8マスの状態がどうなっているかで次の世代のマスの状態が変わります。

プログラムの構造

ライフゲームは、あるマスの周り8マスの状態から次の世代の状態を決定するというルールに従って動作します。

ここでいう世代とは、プログラム上ではループのN回目、N+1回目、などのイテレーションを指します。

世の中にライフゲームのルールは複数あるかもしれませんが、今回は以下のルールで動かしていきます。

• ・あるマスに点がない状態で、周りのマスに点が3つあれば、次の世代でそのマスに点ができる
• ・あるマスに点がある状態で、周りのマスに点が1つ以下あるいは4つ以上であれば、次の世代でそのマスの点はなくなる
• ・上記以外の場合、あるマスの状態は次の世代でも同じとなる

これらのルールの元、ある世代での各マスの状態を調べて次の世代の各マスの状態を表現していく、ということを繰り返します。

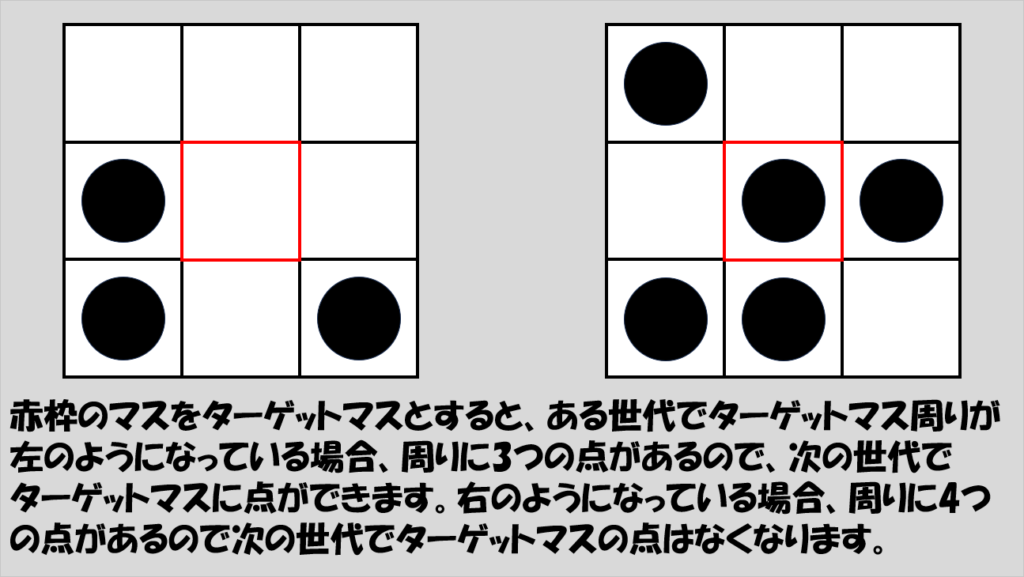
計算を行う上で効率のいいプログラムがあるかもしれませんが、最も単純には、全てのマスを片っ端から計算するという方法になります。

ただしここで注意する必要があるのは、「端」のマスです。

端のマス、例えば左端列のマスたちは、周囲に8マスが存在していません。（例えば左上隅のマスは周囲を3マスにしか囲まれていません）

こういったマスにも、他の、端ではないマスと同じ処理を施すための工夫が必要になりますが、今回は「端を端ではなくする」という処理をしています。

つまり、上下に1行、左右に1列増やすことで、元々の配列で端となっていた行や列を端ではなくします。

一方で、調べるマスの対象は、元々の配列の範囲（下の図右側の、黒いマスのみ）とします。

こうすることで、調べる対象マスは全て周囲を8個のマスに囲まれた状態となります。（上下左右に増やしたマスは点がないマスと見なして演算します）

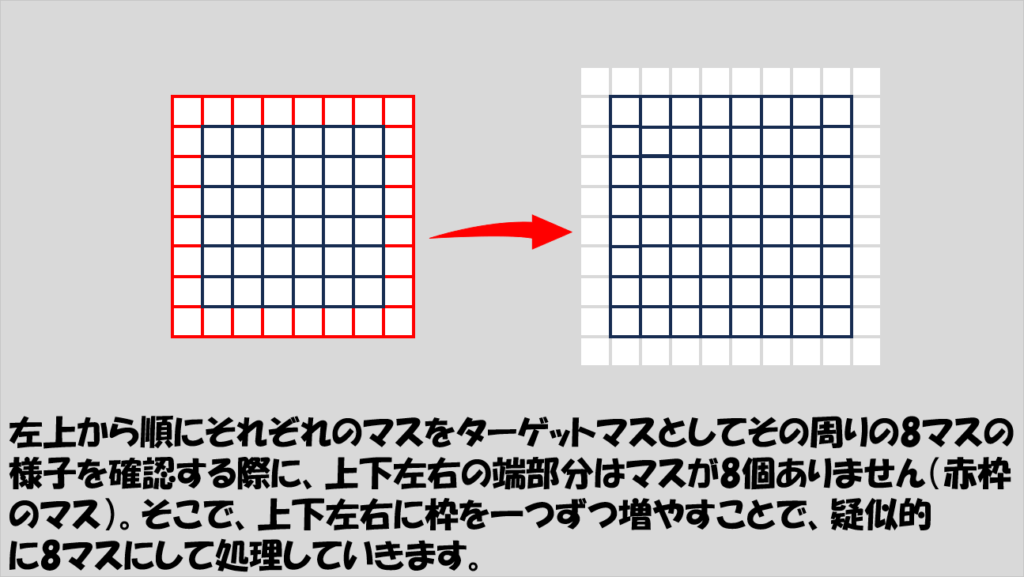
これをプログラムに落とし込んだのが以下の図のブロックダイアグラムです。

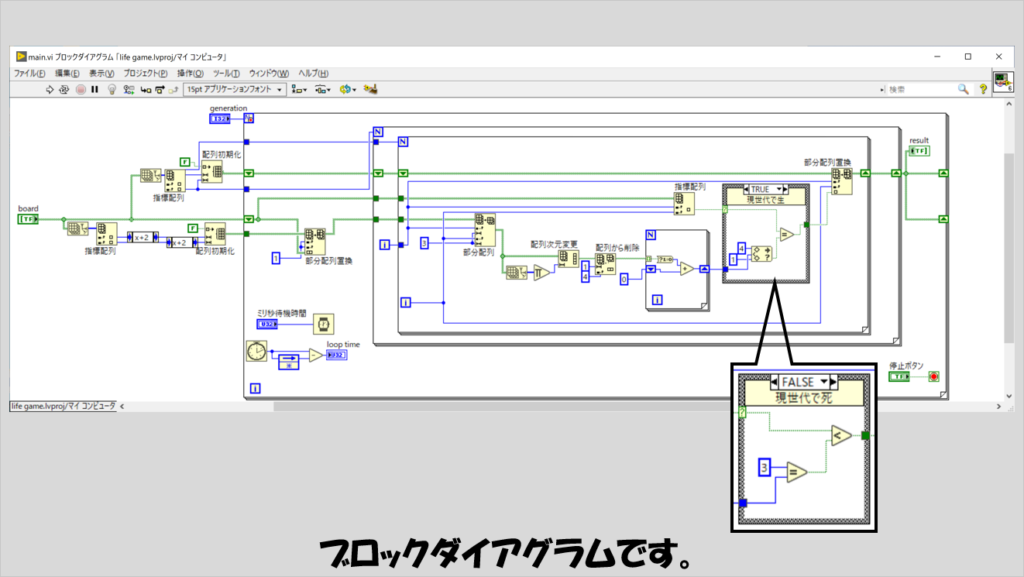
Forループに入る前にしている処理は、上で説明した、「元々の配列の上下左右に1行および1列を追加する」という操作です。

また、配列操作はあらかじめ大きさを決めた配列に対して特定の要素の内容を置換した方が処理の速度的にもメモリ効率的にも都合がいいので、Forループに入る前に「元々の配列と同じ大きさ」の初期化された配列と、「元々の配列の上下左右に1行および1列を追加した、初期化された配列」を用意してこれらをForループで使うこととしています。

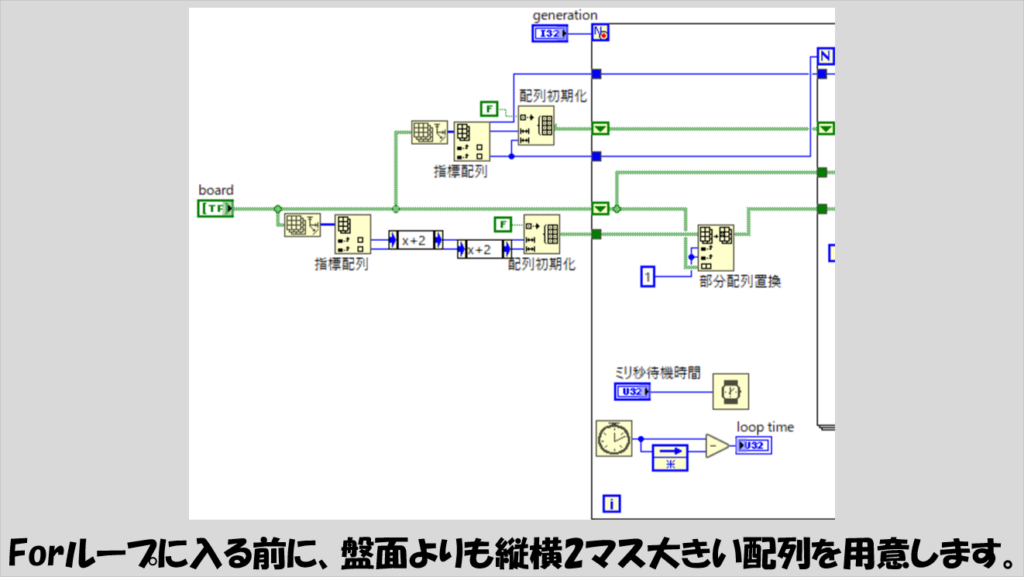
Forループの中では、一つ前のループのときの盤面の様子を元に、各マスで点を作るか否かを判定します。

外から2番目のForループと3番目のForループを使って各マスの状態に着目し、その周辺のマスを部分配列で取得、そこから、「着目しているマス」自身を抜き出して、残りの8個のマスに何個点があるか（Trueがあるか）を数え（これが一番内側のForループ）、その結果と、現在のマスの状態（指標配列で取得）とを元に、現世代で点をつくるか消すか等をケースストラクチャで判定しています。

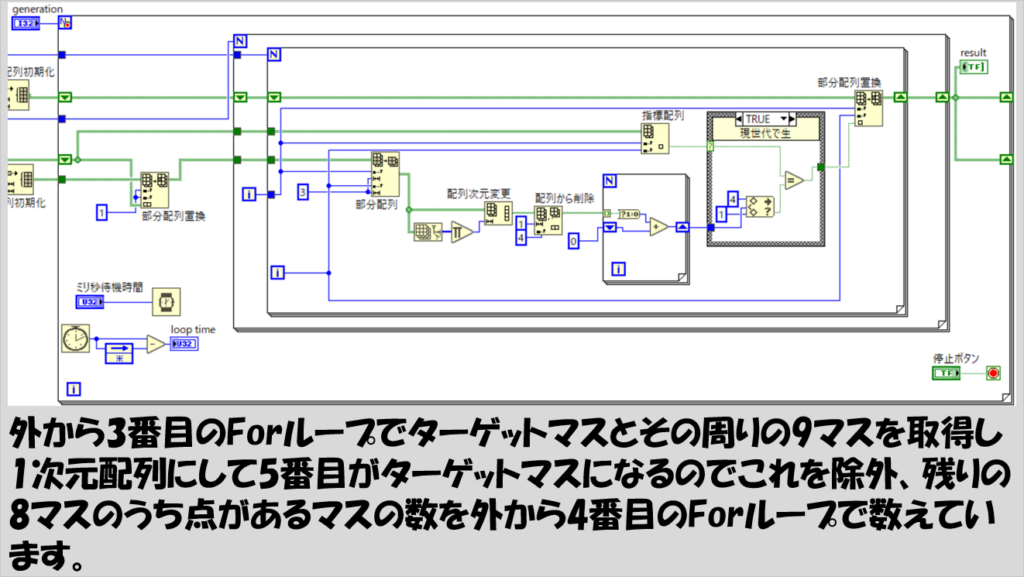
このような、各マスを「しらみつぶし」に調べる方法よりも効率よく判定させる方法はあるかもしれないですが、元々の盤面がそこまで巨大ではない限り、外側のForループ1回はかなり早く終わるので、プログラムの実行速度の面では気にならないと思います。

ライフゲームのパターン

ライフゲームは、あまりに適当に点を配置するとすぐにゲームが終了（全ての点がなくなり絶滅する）こともあるのですが、特定のパターンに落ち着いてその状態から変わらなくなったり、周期的にあるパターンを繰り返したりと、意外と奥が深かったりします。

ネット上にはいくらでもそのような例はあるのですが、以下にいくつか特徴的な結果になる例を紹介します。

固定パターン

何世代化後にある状態になって以降世代が変わってもその形が変わらないパターンで、いくつかの種類があるのですが、例えばこれです。

しかし、一つだけ変えると、あるパターンをいったりきたりするようになります。

移動パターン

移動パターンには、グライダーと呼ばれる形があり、あるパターンを繰り返しながら右下に進んでいきます。

周期パターン

周期パターンで印象的なのは、銀河と呼ばれる形で、銀河系が渦巻く様子を8世代周期で繰り返していきます。

これらがどのような変化をたどっていくかはぜひプログラムを作って確認してみてください。

本記事ではライフゲームを作る方法を紹介しました。

ゲームを通して配列操作を扱うプログラムの例としてはなかなか面白いと思うので、作ってみて実行して気分転換にでもしてもらえればと思います。

ここまで読んでいただきありがとうございました。