この記事で扱っていること
- モンティホール問題をLabVIEWで表現する方法
を紹介しています。
注意:すべてのエラーを確認しているわけではないので、記事の内容を実装する際には自己責任でお願いします。また、エラー配線は適当な部分があるので適宜修正してください。
モンティホール問題は、以下のルールで行うゲームのことで、直感に反した結果となる題材として取り上げられることのある、確率が絡んだお話になります。
- ドアが3つあり、そのうちの一つが「当たり」、2つが「外れ」となっている。
- プレイヤーはその中から1つのドアを選択する。
- プレイヤーが選んだドア以外の2つのうち、「外れ」のドアが一つ開かれる。
- プレイヤーは、最初に選んだドアのままにするか、開かれずに残っているドアにするかを選択できる。
- 「当たり」を引いたら勝ち。
詳細は省きますが、この議論の結論としては、プレイヤーが「開かれずに残っているドア」を選んだ方が当たりになりやすい、という結果となります。
本当にそうなのか?を実際に確かめるゲームを作って遊んでみます。
また記事後半では、自動モード(毎回必ず「開かれずに残っているドア」を選択するようにして当たるかどうか判定することを自動で行う)での実装も紹介します。
どんな結果になるか
フロントパネルには3つのピクチャを配置しており、それぞれが「ドア」となります。
プログラムを実行すると、ステータス画面に現在のゲームの進行状況が表示され、指示通りに進めていきます。
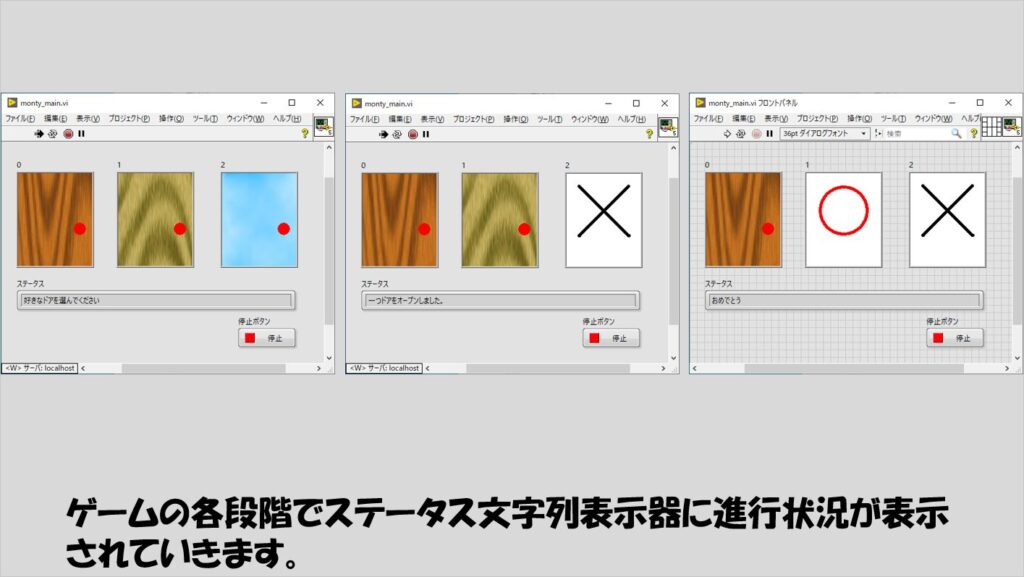
プログラムの構造
プログラムのメインに入る前に、まずはピクチャに表示している「柄」から。
上で紹介した実行時の例のピクチャに表示されている模様、見覚えがないという方が多いかもしれませんが、これはLabVIEWインストール時に使用できる、フロントパネルの背景として設定できるjpg画像からきています。
C:\Program Files (x86)\National Instruments\<LabVIEW version>\resource\backgrounds
のパスにあるので、もし同じ柄を使用する場合には例えば以下のようにピクチャにあらかじめ設定しておきます。
Draw Oval.viと書いてあるのは楕円を描くための関数で、今回はドアノブを表現しています。
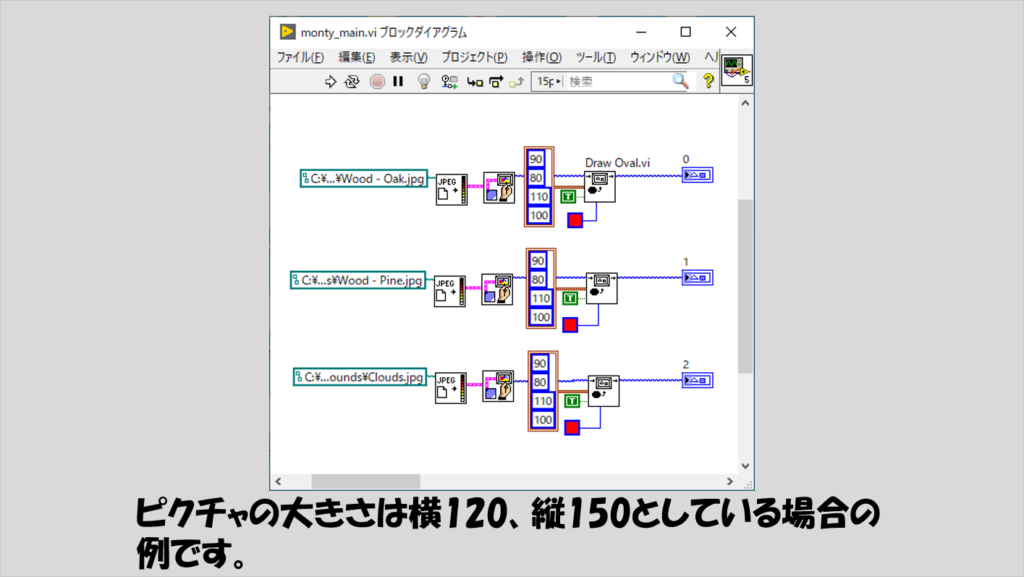
ではメインのプログラムに入っていきます。
段階ごとにユーザーの操作が必要になるプログラムで、イベントストラクチャを使用していますが、今回はプログラムも大きくはないためイベントストラクチャの中にステートマシンの要素を加えてみました。
つまり、タイムアウトイベントの中にケースストラクチャを設けてここをステートマシン風にしています。
ステートマシン全体で使用するデータとして、「success」と「select」の二つの列挙体が入ったクラスタを用意しています。
列挙体の要素は「0」、「1」、「2」の3つが入っています。
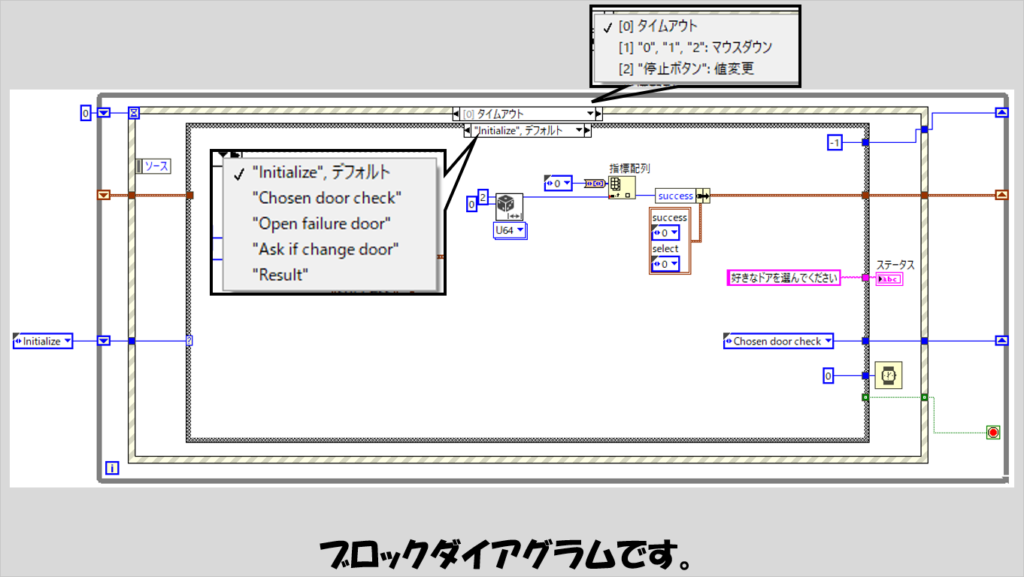
ステートマシンの説明に入る前に他のイベントの内容を紹介していきます。
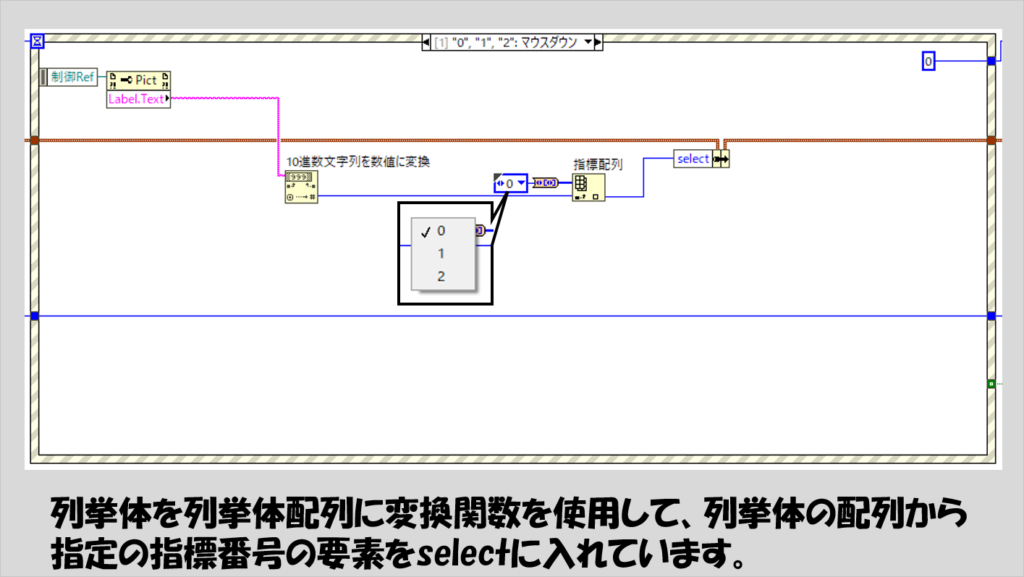
ピクチャにそれぞれ0、1、2というラベルを付けており、これらのマウスダウンイベントを用意しておきます。
ピクチャのラベルを数字にしておくと、イベントデータノードから操作が行われたピクチャのリファレンスが取得でき、ここからプロパティノードでラベルテキストを拾うことができます。
このラベルテキストは0、1、2が文字列となっているのでこれを数値に変換し、その後に指標配列の関数に渡しています。
指標配列の関数では、ステートマシン全体で使用するクラスタの要素になっていた列挙体に対して「列挙体を列挙体配列に変換」関数の結果としての配列から特定の要素を取り出すようにしています。
「なんでここでわざわざ列挙体にする必要があるの?そのままラベルテキストを数値に変換した数値を扱えばよくない?」と思うかもしれませんが、理由は後から出てきます。
なお、右上に見える定数0は、タイムアウトイベントの時間を指定しているので、ここが0ということは「このイベントが実行されたらすぐにタイムアウトイベントが実行される」ことを意味します。
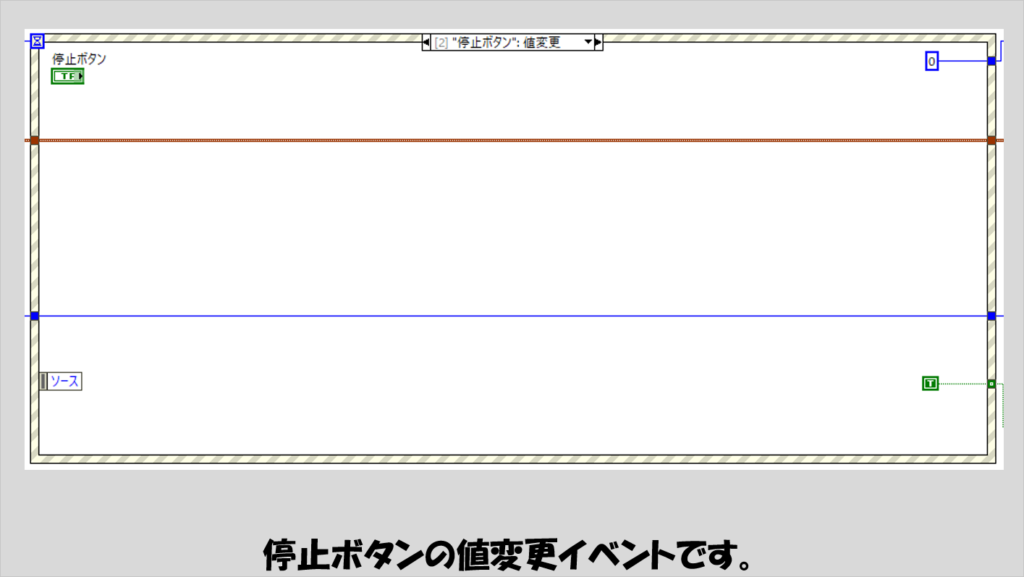
もう一つ、イベントとしては停止ボタンの値変更イベントを用意しています。
これは単にプログラムを終了させるためのイベントです。
では、タイムアウトイベントの中身に入っていきます。
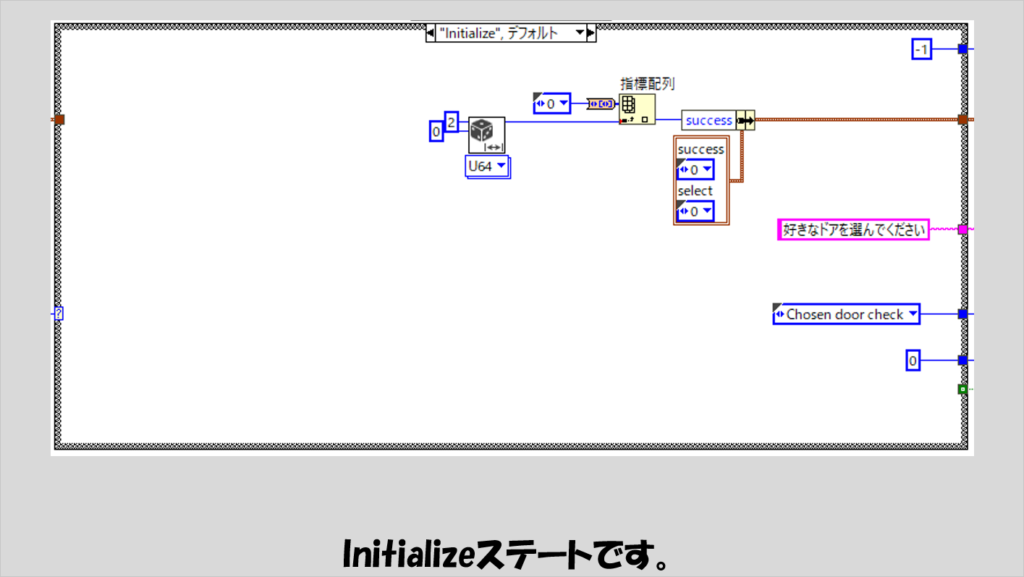
まずはInitializeステートです。
ここでは、まず「正解のドア」をsuccessとして決めています。
乱数で0か1か2を決定し、ここでも列挙体配列から要素を指定してクラスタのsuccessに入れています。
このステートの後は、右上に定数-1があることから、タイムアウトイベントは発生せず、ユーザーがいずれかのピクチャを選ぶのを待ちます。
一方で、次のタイムアウトイベント時にはChosen door checkステートに進むように指定もしています。
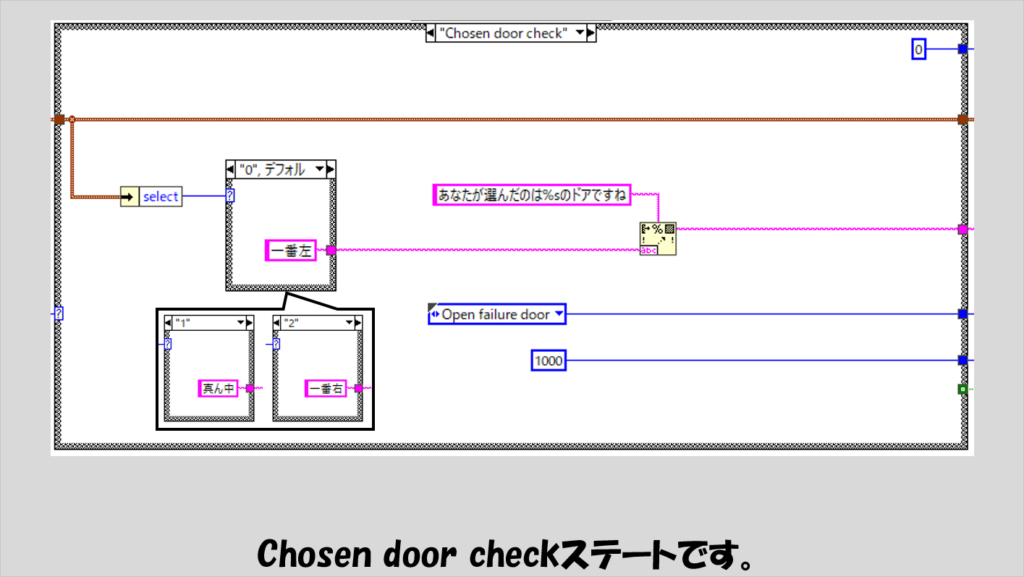
次にChosen door checkステートでは、この直前に実行されているはずである、ユーザーによるドアの選択(3つのピクチャへのマウスダウンイベントの結果)の内容を確認するメッセージを表示します。
ユーザーが指定したピクチャはクラスタのselectに入っているはずで、その内容から、どのドアを選びましたね、という確認メッセージを表示します。
このあとはOpen failure doorステートにすぐに移ります。
Open failure doorステートでは、ユーザーが選んでいないドア2つのうち、必ず不正解のドアを選ぶ必要があります。
ここで、ユーザーが最初に選んだドアが正解のドアか、不正解のドアかで処理が変わります(下の図の、selectとsuccessが等しいかを判定した後のケースストラクチャで分岐します)。
そしてこの処理選択後の分岐を簡単にする点に、selectやsuccessで列挙体を使ってきた理由があります。
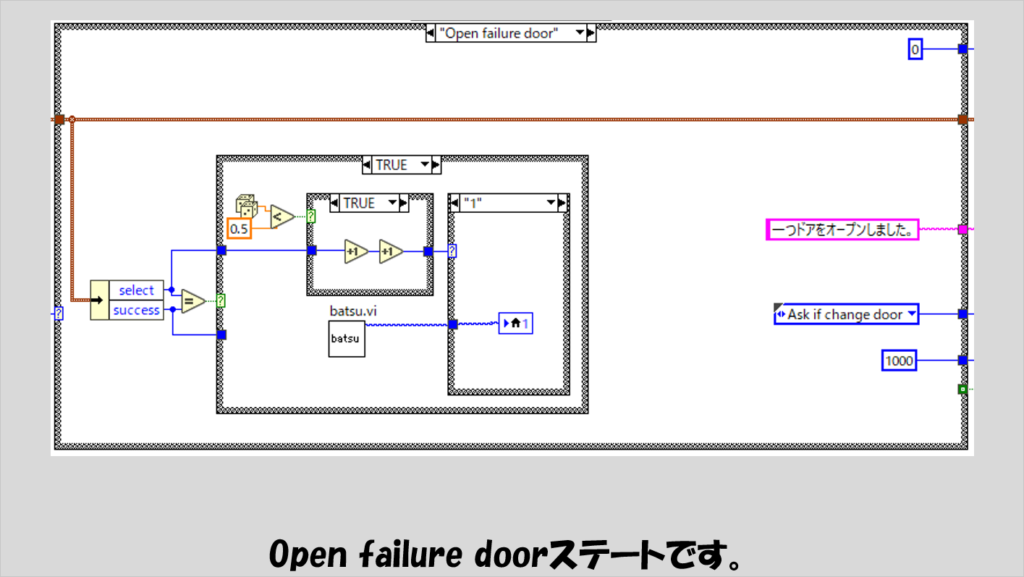
列挙体は、LabVIEW内部では数値として扱われています。
数値ということは、足し算ができるのですが、特にインクリメント関数を使用した場合、「循環する」という特徴があります。
今回の例で言えば、列挙体に登録している項目は、「0」、「1」、「2」の3つで、「0」の時にインクリメントすると「1」に、これをインクリメントすると「2」になりますが、さらにインクリメントすると「0」が選ばれる、ということです。
(インクリメントではなく、和の関数で1を足してもこうはならないので注意。和の関数を使用する場合、強制ドットがついて、データタイプの強制変換が行われることが原因のようです)
これを踏まえ、このOpen failure doorでの処理を考えていきます。
まず、ユーザーが最初から正解のドアを選んでいた場合です。
このとき、Open failure dootとして、開く「不正解のドア」一つを選ぶには、「ユーザーが選んだドアの番号の列挙体にインクリメントを1回するか2回する」ことで全てのパターンに対応できます。
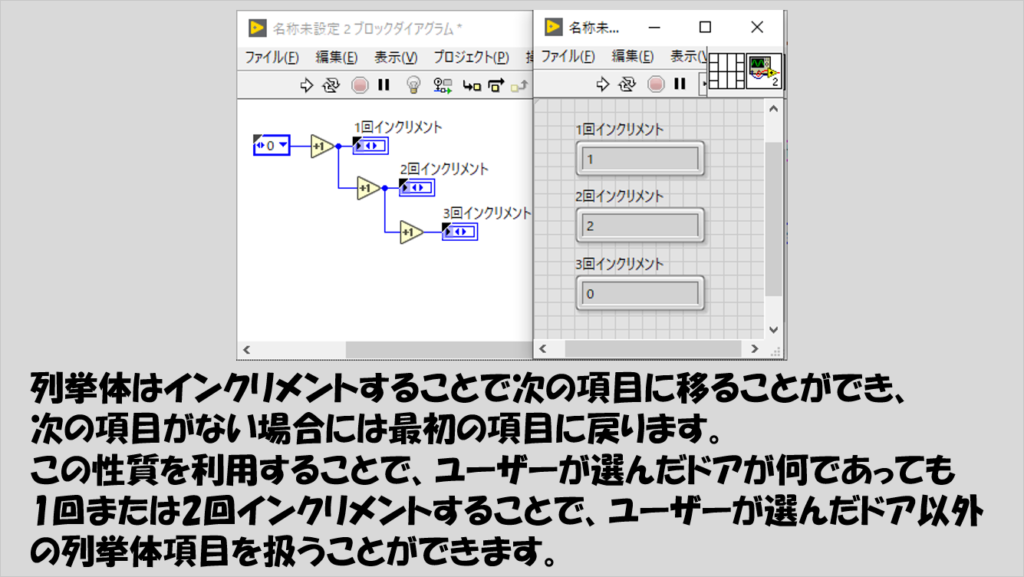
例えば正解のドアが「1」でユーザーも「1」を選んだ場合、不正解のドアは「0」と「2」ですが、これらは、「「1」となっている列挙体にインクリメントを1回すると「2」に、インクリメントを2回すると「0」になる」ことを利用しプログラム的にランダムで選ばせます。
ここを列挙体ではなくただの数値でやる場合、ケースストラクチャの場合分けが「正解が0だった場合」「1だった場合」「2だった場合」の3つになり、分岐の種類が多くなってしまいます。
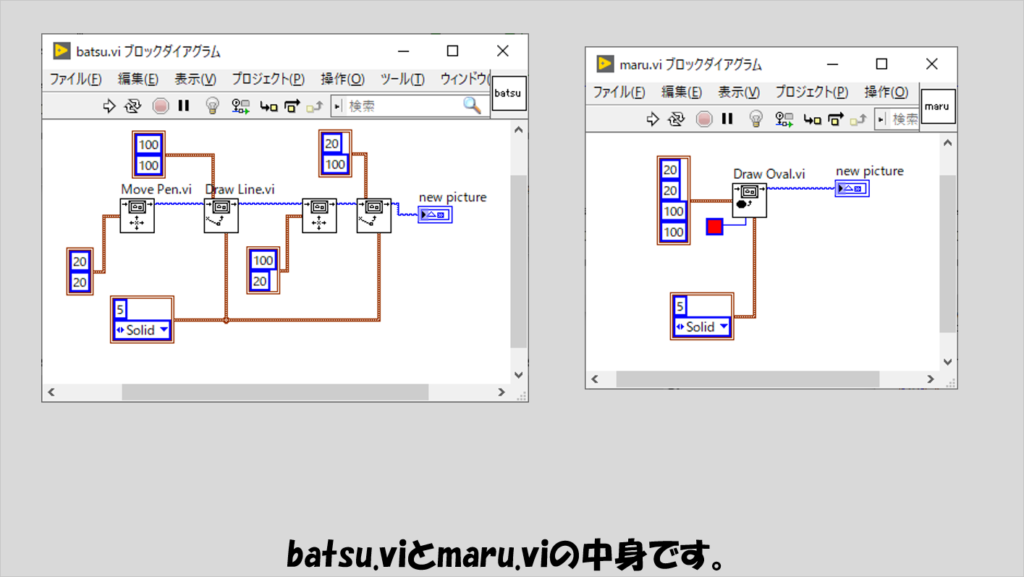
不正解のドアとして開くドア一つをプログラム的に決めたらそのドアのピクチャに対して×マークを記すために後述するbatsu.viを使用します。
今度は、ユーザーが最初に選んだドアが正解のドアではなかった場合を考えます。
このとき、残った2つのドアのうち不正解のドアを指定するには、「3 – (正解のドアの数) – (ユーザーが最初に選んだドアの数)」という計算を行います。
例えば正解のドアが0でユーザーが最初2のドアを選んでいた場合、3 – 0 – 2で1と判断できます。
ここでも列挙体が数値として扱える性質を利用しています。
だいぶ説明が長くなりましたが、これらを踏まえOpen failure doorを実行します。
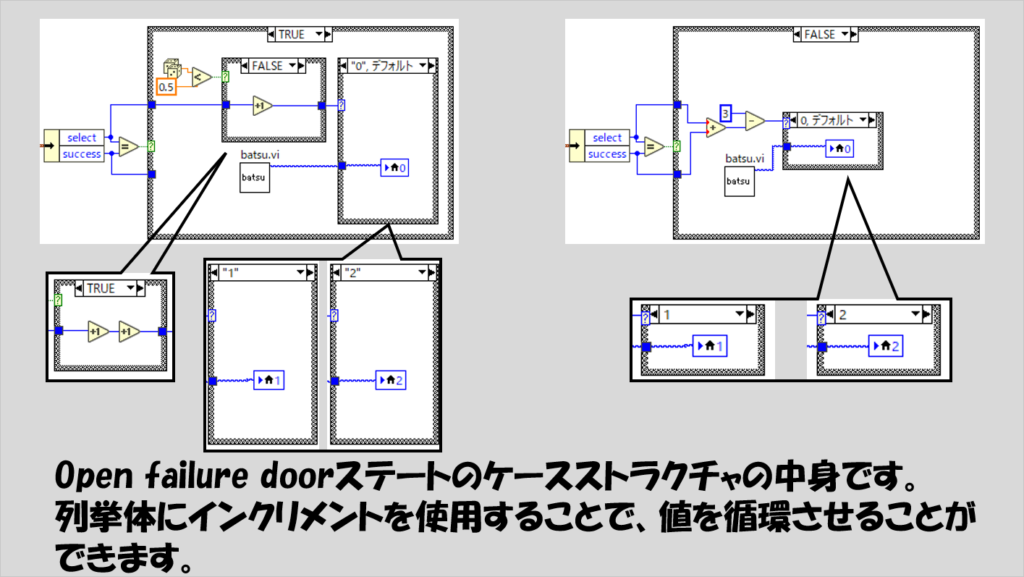
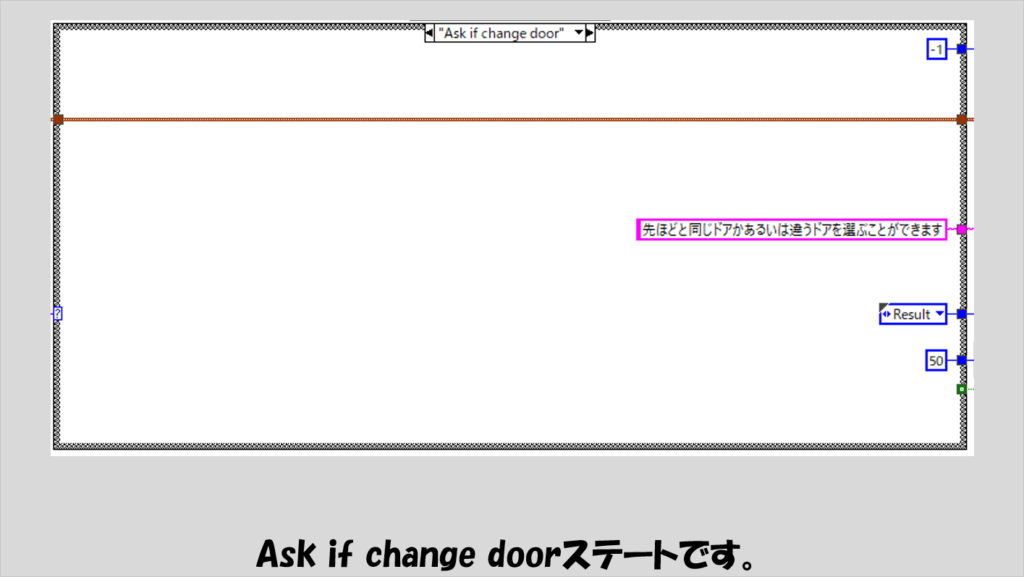
次のAsk if change doorステートでは、ユーザーにドア変更のチャンスを与えます。
このステートの後にはユーザーの操作が入ることから、右上の定数は-1としてタイムアウトイベントが起こらないようにしています。
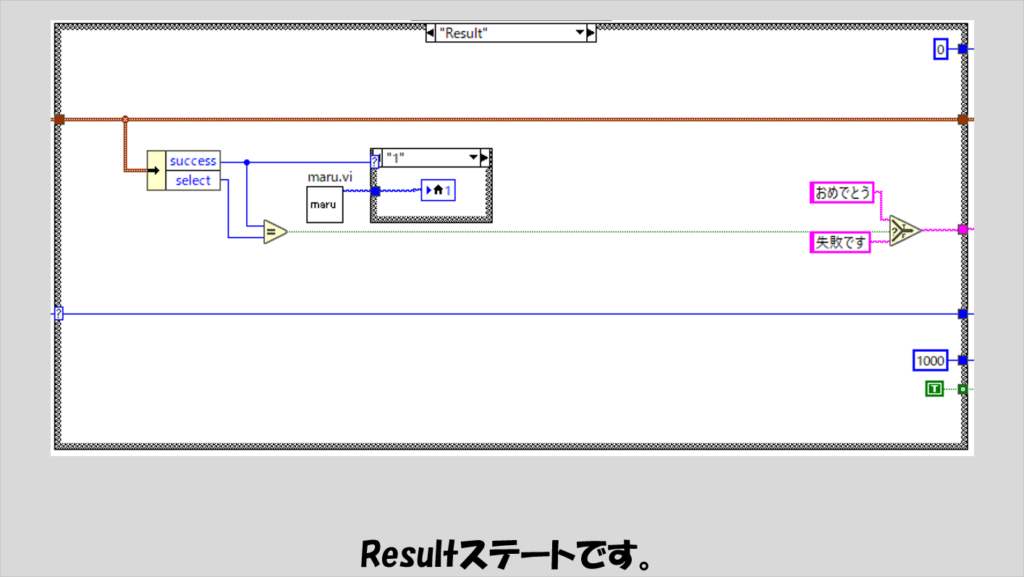
Resultイベントでは、正解のドアに対してmaru.viの出力を各ピクチャ(のローカル変数)に渡します。
以下の図で中のケースストラクチャの全てのケースを表していませんが、Open failure doorでbatsu.viを使用したのと同じ要領なので割愛しています。
また、successとselectが一致しているかどうかでユーザーが正解のドアを選んだかどうか判定できるので判定した結果のブールを選択関数に入れて表示するメッセージを選択しています。
これまでに出てきていたbatsu.viとmaru.viは以下を参考にしてください。
(別にこれである必要はなく、正解、不正解がわかればなんでもいいのですが)
自動モードでの実装
上記はユーザー(人間)が実際にピクチャを選んで当たるかを見ていましたが、これらの操作を自動で行わせるようにします。
なぜ自動で行わせるようにしたかというと、もともとは「1番最初にドアを選んで、その後不正解のドアが開かれてから、次に選ぶドアを最初に選んだドアではないものにしたときに当たる確率」(理屈の上では2/3の確率で当たる)がどうなるかをシミュレーション的に見たかったためです。
ただ、ここまでの実装で気づいている方がいるかもしれませんが、これは実際にプログラムを実行して確かめなくても2/3の確率になるはずということが直感的にわかると思います。
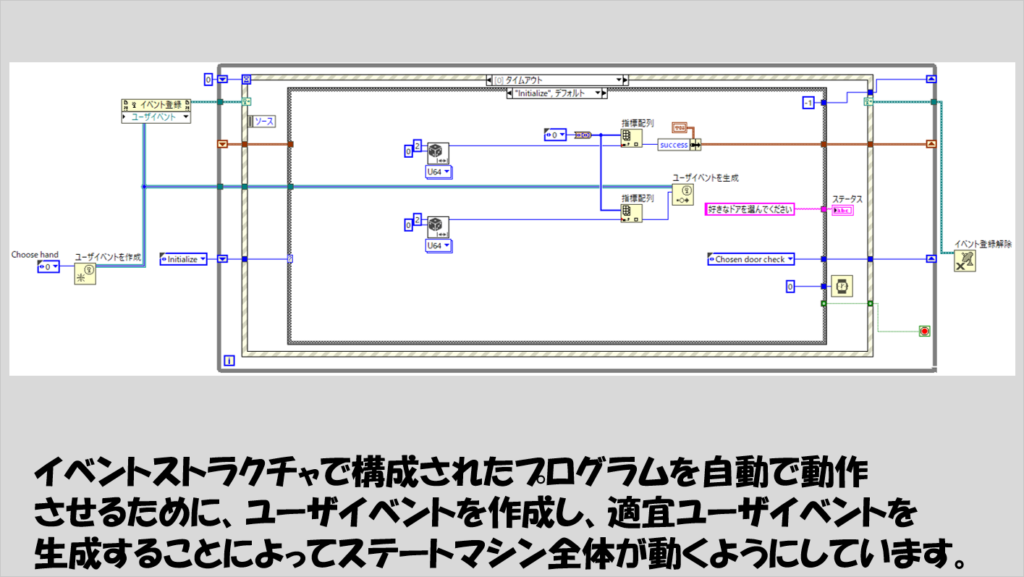
なお、上記での実装はイベントストラクチャをベースにしていたので、これをどう自動化するか想像がつかないという方もいるかもしれませんが、プログラム的にイベントを発生させるためにユーザーイベントを使用すれば割と簡単に自動化できます。
ユーザイベントを生成時に指定するデータタイプは、上のプログラムで何度も出てきている、「0」などの要素が入った列挙体としています。
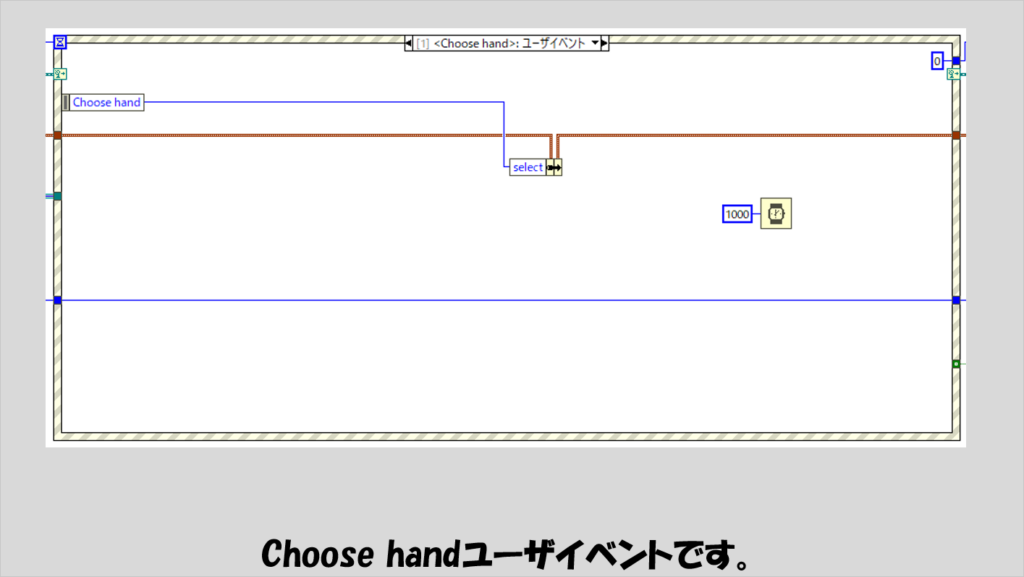
ユーザイベントとしては、Choose handイベントデータノードの値をクラスタのselect要素に入れています。
タイムアウトイベントで修正するべきステートマシンのステートを見てみます。
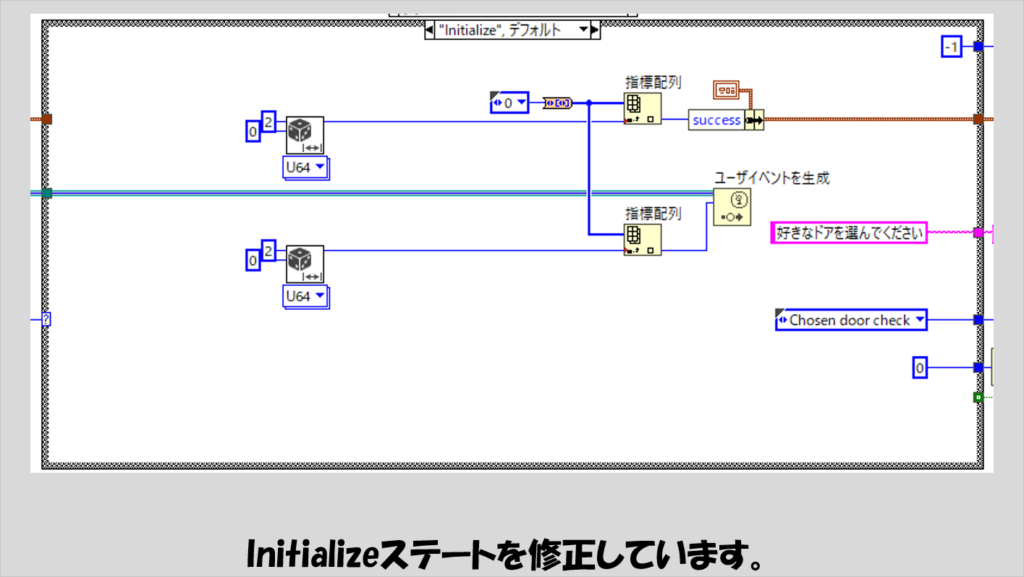
まず、Initailzeイベントでは、早速ユーザイベントを生成していきますが、こちらもまた乱数の値を指標番号として指標配列関数に配線し、列挙体配列から選ぶようにしています。
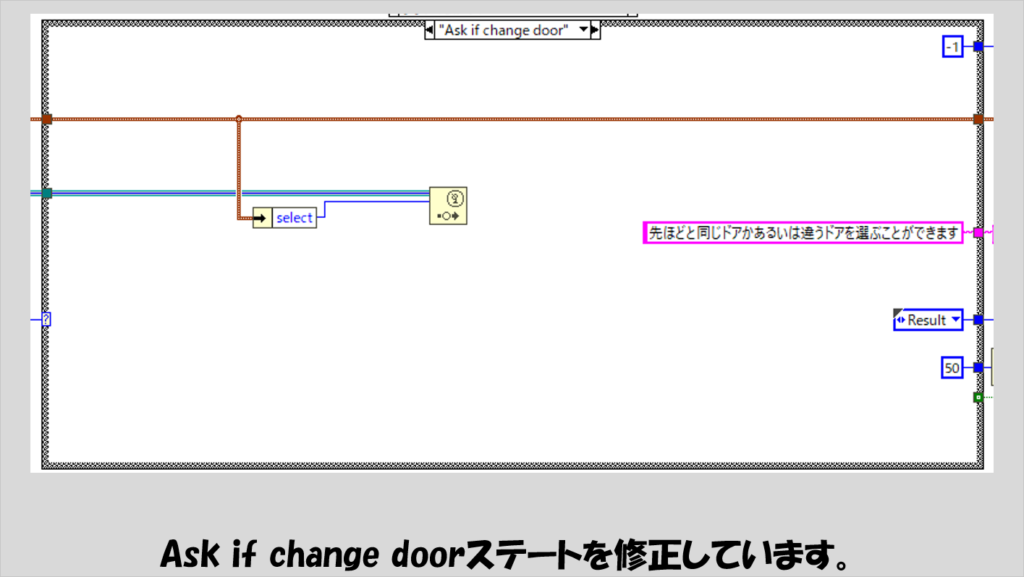
Ask if change doorステートも以下のように変えます。
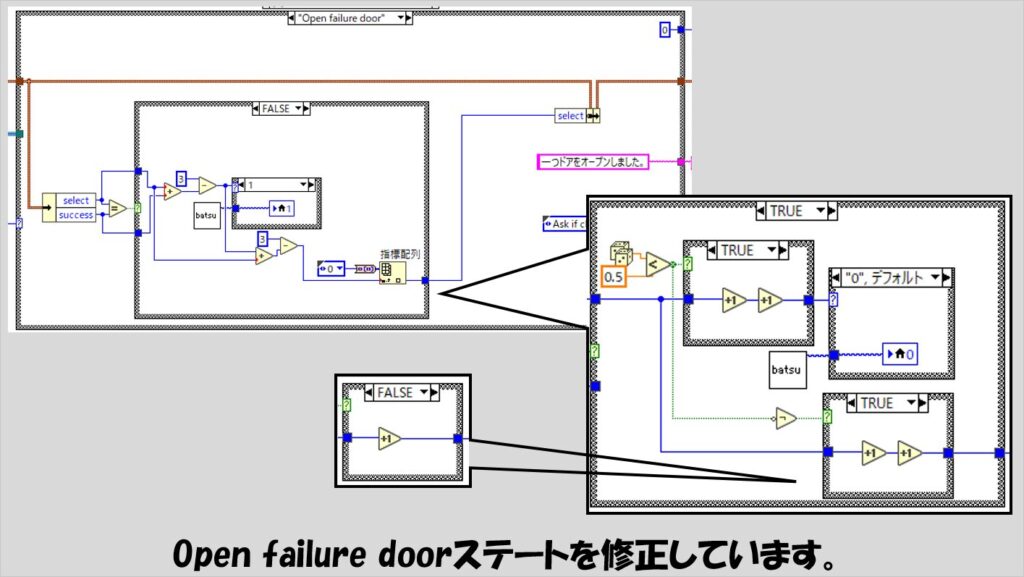
Open failure doorステートも以下のように変えます。
実はこの時点でプログラム的に行わせている処理を見ると、「1番最初にドアを選んで、その後不正解のドアが開かれてから、次に選ぶドアを最初に選んだドアではないものにしたときに当たる確率」が2/3であることがわかります。
なぜなら、今回のプログラムでは、最初に選んだドアが不正解のドアであった場合には、1つ開かれるドアは必ずもう一つの不正解のドアが選ばれて、その後に最初に選んだドア以外のドア、つまり正解のドアが選ばれるという操作を行っているため、逆に言えば「最初に選んだドア」が正解のドアか不正解のドアかで最終的な結果が確定してしまうためです。
最終的に(2回目ドアを選んだときに)正解のドアを選ぶというのは、最初に選んだドアが不正解のドアであるのと同値になります。
ドアは3つあってそのうち正解のドアは1つなので、不正解のドアを選ぶのは2/3、ということで、シミュレーションを行わなくても確率が求まります。
結果的にこの自動的に処理を繰り返す意味はなくなりましたが、ユーザイベントを駆使してイベントベースのプログラムさえもある程度自動化したプログラムにするための練習としては悪くないと思っています。
本記事ではモンティホール問題をLabVIEWで表現する方法を紹介しました。
自動化の部分はともかく、「2回目に選ぶドアは、1回目に選んだドア以外にした方が当たる確率が高くなる」というのは何となく不思議な感じがする減少かなと思うので、これを実際に確かめるゲームとして考えると面白い題材だと思います。
ここまで読んでいただきありがとうございました。


コメント