この記事で扱っていること
- スターウォーズのように流れる文字を作る方法
を紹介しています。
注意:すべてのエラーを確認しているわけではないので、記事の内容を実装する際には自己責任でお願いします。また、エラー配線は適当な部分があるので適宜修正してください。
この記事が公開されている前日は5月4日、May (the)4thということで、スターウォーズの日でした。
スターウォーズの映画の最初、ロゴが表れてから流れるオープニングクロールは、壮大な宇宙に黄色い文字が流れ画面の奥に消えていく、とても印象深い演出だと思います。
あれ、かっこいいですよね。
というわけで、あのような文字表示を行うための仕組みを作ってみます。
実用アプリでこの文字表示を直接何かに役立てるということはほとんどないと思いますが、実は考え方としては「疑似3D」を作ることにつながり、この疑似3Dについては2次元空間を3次元っぽくみせる、より面白いアプリケーションにつながります。
そんな、より面白いアプリケーションについては別の機会で紹介したいと思います。
どんな結果になるか
画面にはピクチャ表示器があり、スターウォーズのどのエピソードのオープニングクロールを表示するかを指定する数値制御器があります。
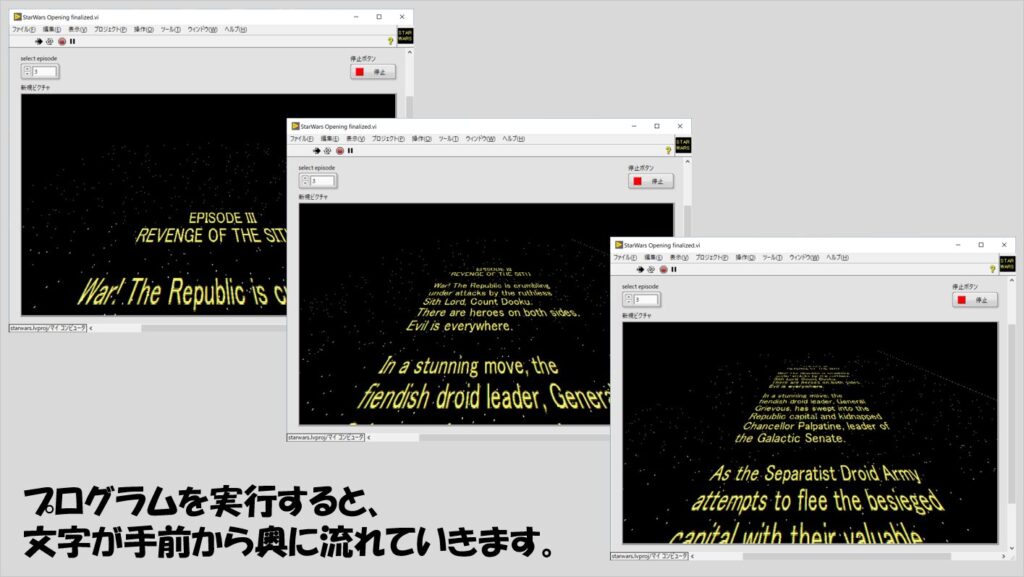
プログラムを実行すると、文字が自動的に流れ、手前から奥に向かって流れていきます。
当然、表示する文字列は自由に決められるので、スターウォーズとは全く関係ない言葉でも自由に表示できます。
プログラムの構造
上で紹介した動作を行うプログラムをそのまま書くだけなのであれば、以下のようにかなりシンプルに書くことができます。
文字を表示させるだけなのに、フォーミュラノードで、しかも三角関数による演算が出てきます。
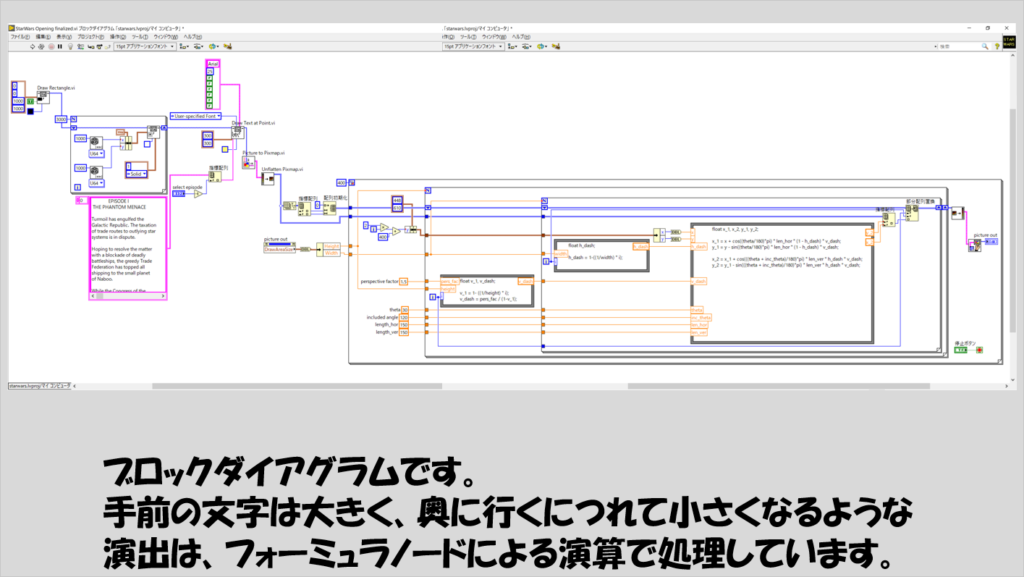
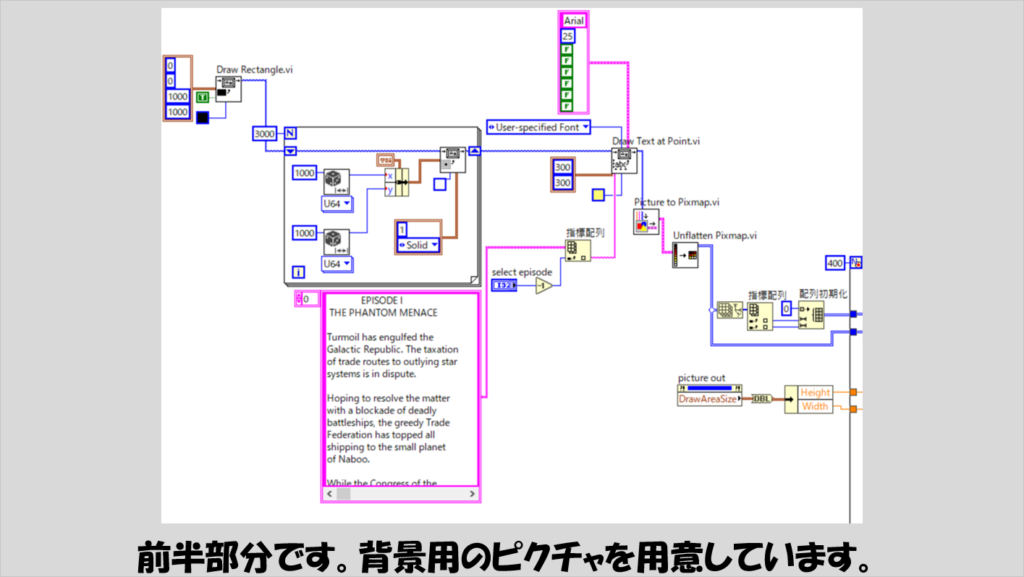
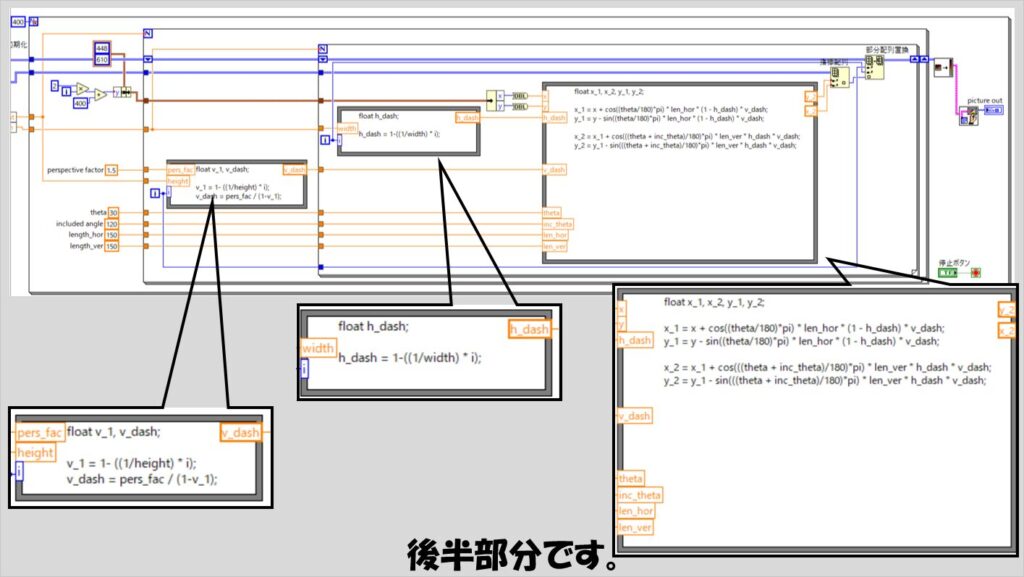
プログラムの前半部分は、背景となる宇宙空間および星々を表現するための仕組みです。
この部分は必須ではないので別になくても構いません。
文字列定数の配列には、各スターウォーズのエピソードの最初に流れるメッセージを入れています。
メインの処理は以下の2重Forループ部分になります。
フォーミュラノードの部分は少しでも間違えると実行できなかったり実行できても期待した表示結果になりません。
thetaやincluded angle、length_hor、length_varそしてperspective factorなどの定数は一例です。
それぞれの定数の値を変えると見え方が変わるので試してみてください。
なぜこれらの計算を行うことで流れていく文字が表現できるようになるかは数学的な知識を少し必要とします。
数学の話なんて見たくない、という方は、計算部分はもう上で紹介したとおりに実装して、あとは文字を変えればもちろん任意の文字に対して同じような演出ができます。
数学の話をぜひ見たい、という方は次の章でこのプログラムで使用されている計算の背景を紹介しているので見てみてください。
どのような計算をすればできるのか
さて、具体的な実装は上で紹介した通りですが、紹介したプログラムの中にあった計算式はどのような数学的背景があって得られたものなのか、についてここで紹介していこうと思います。
これから説明する内容は自分で考えたものではなく、以下のビデオを大いに参考にさせてもらいました。
なので、以下の説明は、このビデオの内容をLabVIEWプログラムに落とし込んだ場合の例と思ってみてください。
(なお、私は特別数学に長けているわけではないため、表現など適切ではない場合があります。ご了承ください)
まず、ピクチャ内のある領域について、「視野」の範囲に見えるものを別のピクチャに表現することを考えます。
つまり、例えば元となるピクチャ上に立ってそれをある視野角の範囲で見たときにそれがどう見えるか、ということを考えていきます。

なぜこのようなことを考えるかというと、結局文字が流れていくというのは、そのピクチャ上に立って、ピクチャ画面が奥に流れる、あるいは見ている人が後ろに下がっていくときに見えている様子尾と同じと見なせるため、まずは立っている人の視界を再現してみようというわけです。
いわゆる遠近感があり、近くの物は大きく、遠くのものは小さく見えるという状態をそのまま再現しようと考えます。

このようなときに有効なのが、高校数学で習った「ベクトル」です。
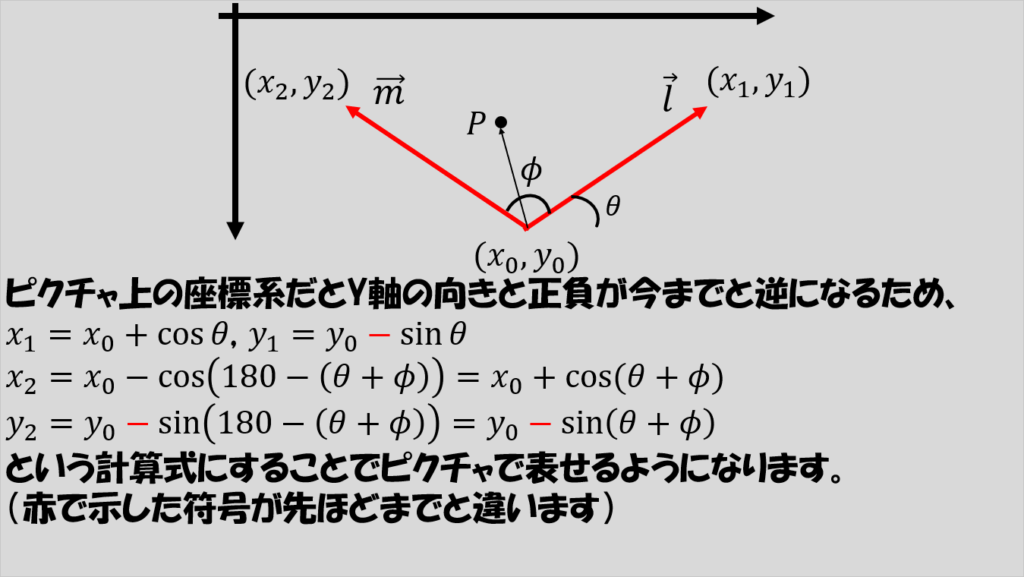
例えば、視野角をΦ度だったとして、X軸とY軸からなる2次元平面上で視野の様子を次のように表せます。
二つのベクトルをそれぞれl、mと呼ぶことにして、これらが単位長さ(長さが1)であるとしたとき、二つのベクトルの交点の座標(x_0,y_0)と、lベクトルの先端位置(x_1,y_1)およびmベクトルの先端位置(x_2,y_2)について以下の関係式が成り立つことがわかります。
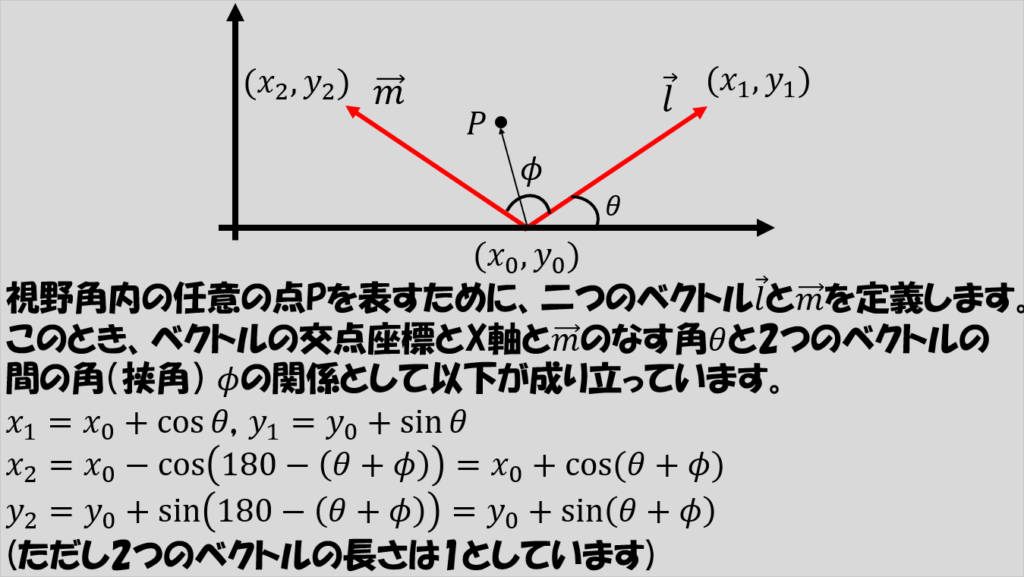
高校のときに、三角関数って何に使うんだろう、と思われた方、こういうときに使いますよ。
これらのベクトルを使用すると、視野の範囲上の座標はlベクトルとmベクトルを用いて
P=(1-h)vl+hvm (0<h,v<1)
と書き表すことができます。
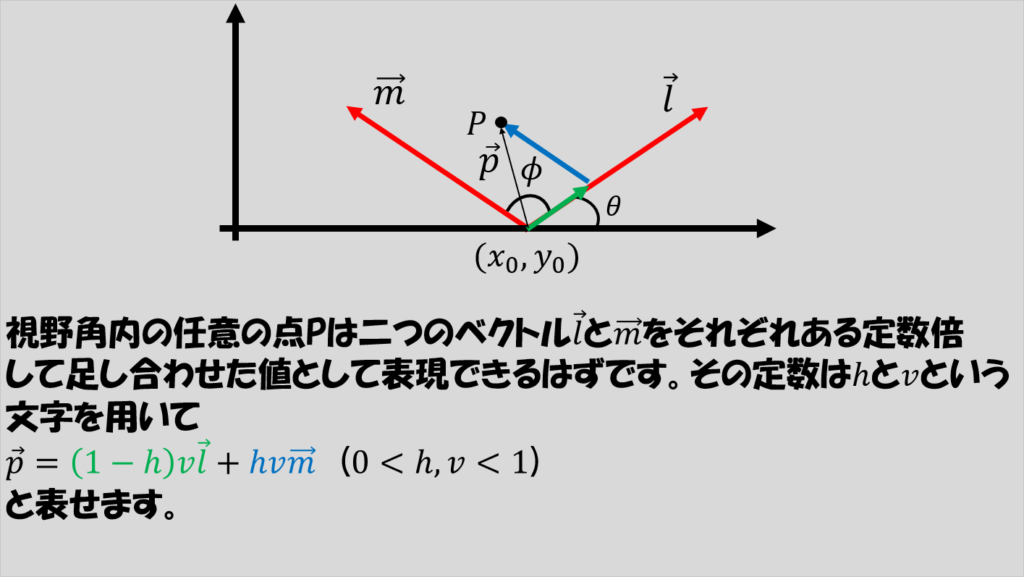
いやいやhとvってなんなのさ、と思われるかもしれないですがl、mベクトルの長さを調整するパラメータで、hを調整するとpベクトルは角度方向に動き、vは長さ方向に動きます。
そのため、hやvをどちらも0から1の範囲で変化させることで、視野範囲のどの領域も表すことができるようになります。
この説明ではよくわからない、という方も多いかと思いますが、こういうときは、具体的な値を代入してみるとわかりやすいと思います。
以下では、h=0を代入していますが、h=1を代入しても似たようなことがわかるかと思います。
また、後でLabVIEWでこの部分のプログラムを書くので、実際に作ってみて様子を確かめるのもアリです。
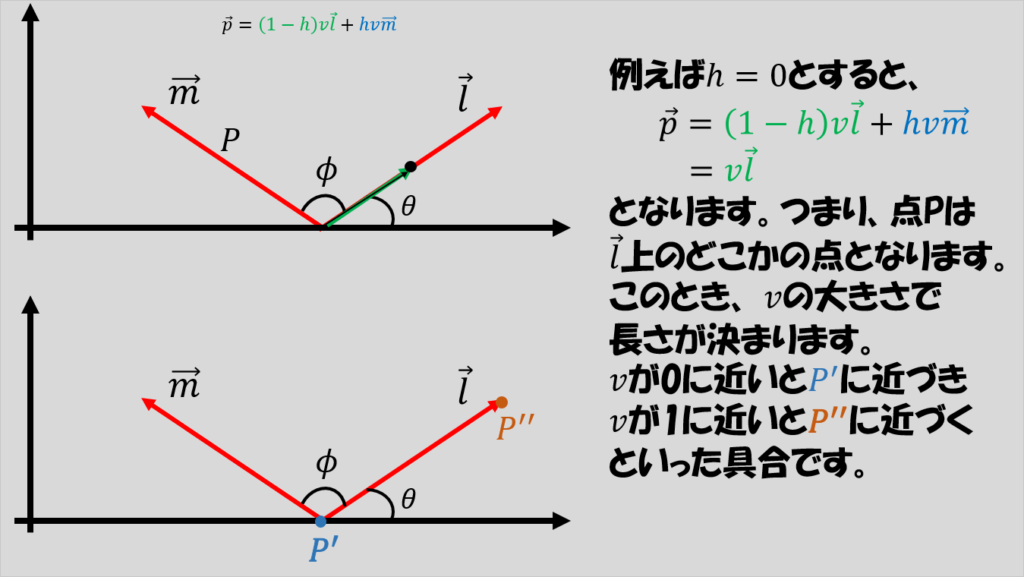
改めて、視野の範囲を2次元平面に表すことを考えると、以下の図のように、それぞれの点を対応させればいいことがわかると思います。
遠くの情報を表す(vが1に近い)ときには、横方向(hが変化したときにとりうるX軸方向の範囲)は広いですが、近くの情報を表す(vが0に近い)ときには横方向は狭くなります。
hのとりうる値の範囲が同じ時、遠くの情報はhが少し変わっても横軸方向に大きく変わる一方で、近くの情報はhが少し変わった程度では横軸方向にほとんど変化しません。
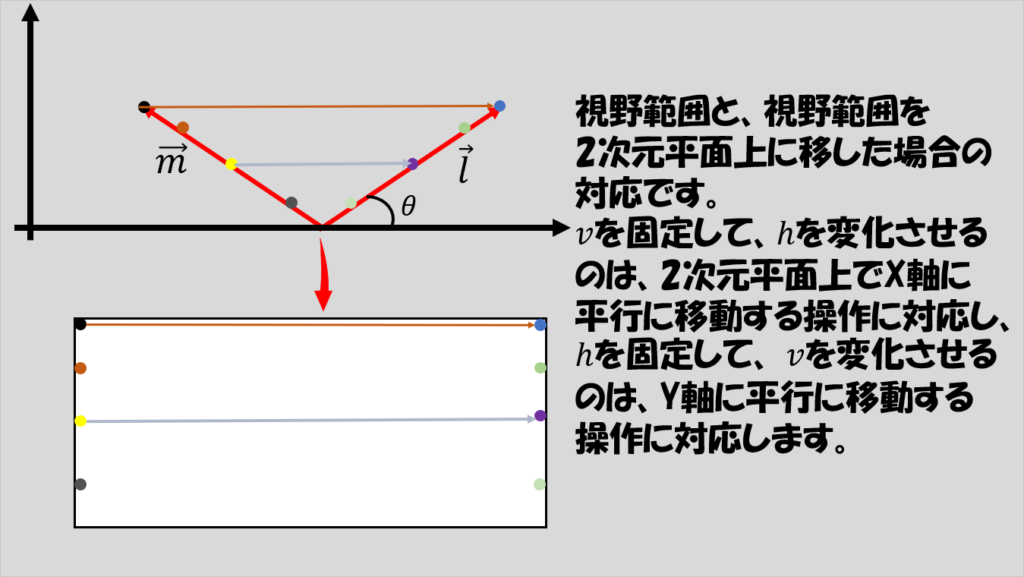
hやvを調整してピクチャ上のそれぞれの点のピクセル値を抜き出し、これを対応する2次元平面上の(x,y)の位置に当てはめれば、視野範囲の値は全て取得することができるようになります。
もしこれまでの流れをLabVIEWで確認したいということであれば、上で書いた通りのことをLabVIEWに落とし込むだけです。
ただし、ピクチャの座標系は今まで説明した「右に行くほどxが大きく上に行くほどyが大きく」という向きではなく、「右に行くほどxが大きく下に行くほどyが大きく」というy軸の向きと正負が逆になっていることを考慮する必要があります。
これらを踏まえて、今までの内容を落とし込んだこんなプログラムを作ってみます。
これを動かすことで、hやvを動かしたときにピクチャがどのように変化するかを確認することで理解を深めることができると思います。
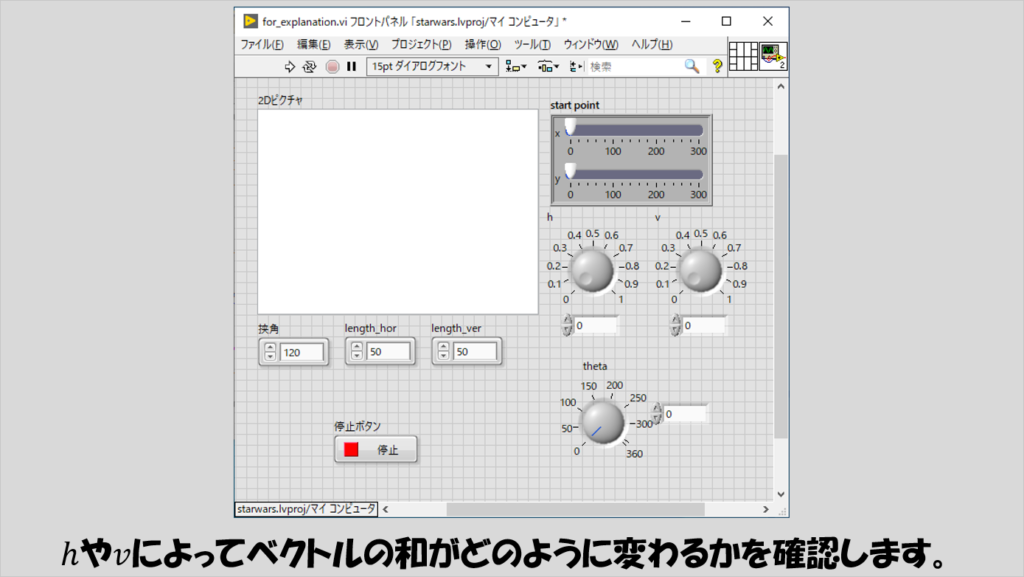
このようなプログラムを作ると、視野角の様子と、hやvを変化させたときにlとmベクトルの和(上の図で出てきたpベクトル)がどのような変化をするかを確認しやすくなります。

ブロックダイアグラムは以下のようにしています。
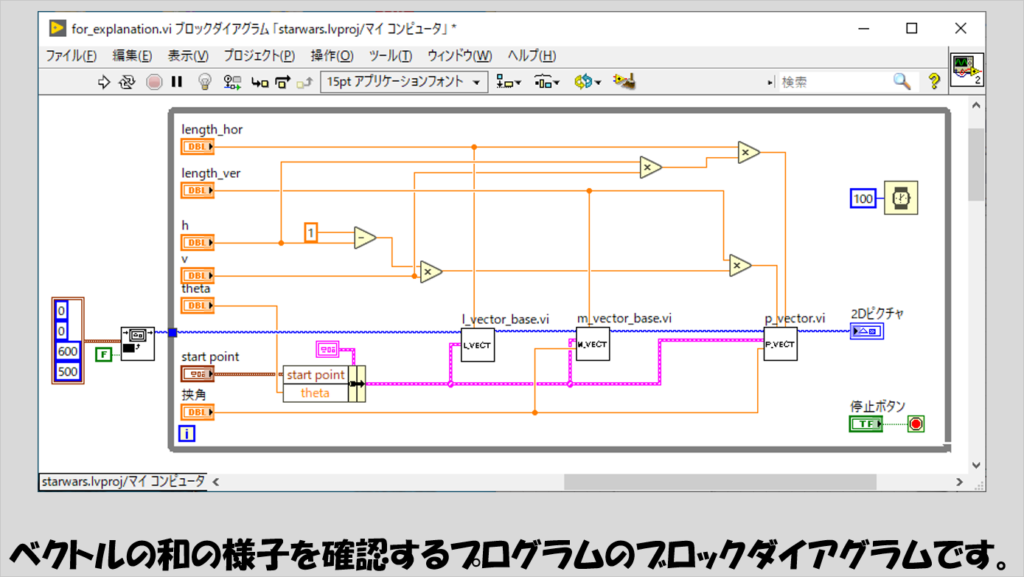
ブロックダイアグラムで使用しているサブVIの中身は以下の通りです。
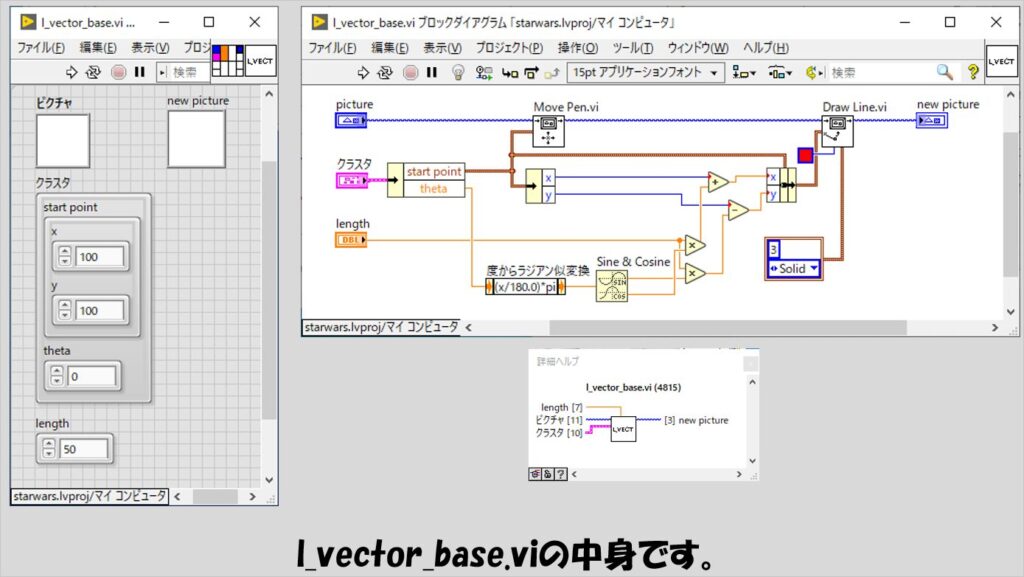
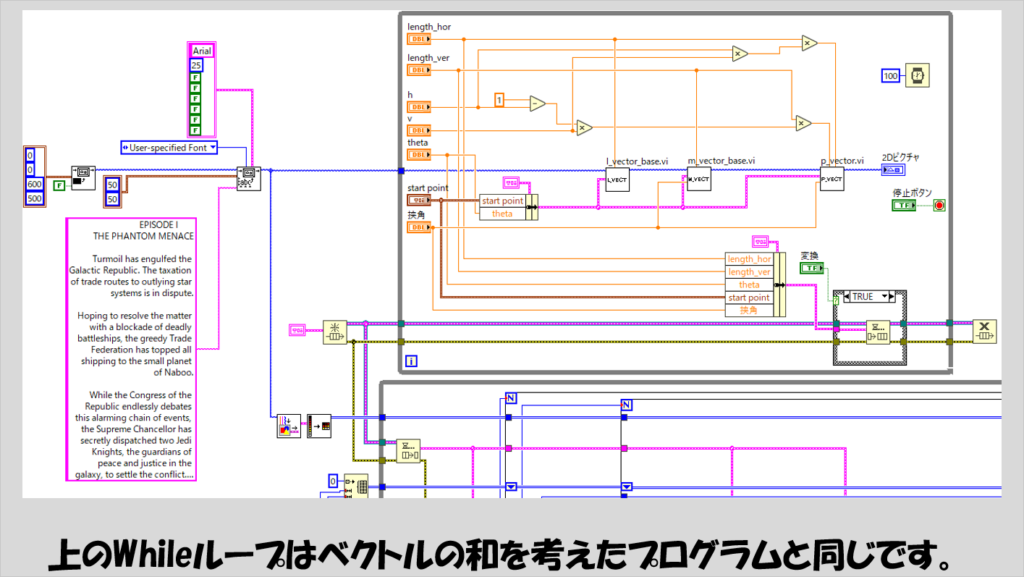
まずは、l_vector_base.viです。
先ほどからの説明でlベクトルと書いていたものを表現するための線を表します。
なお、先ほどの説明ではベクトルの長さを単位長さでやっていましたが、ピクチャ上に表現する際に単位長さだと小さくなりすぎるので、長さを変えられるように入力パラメータとしてlengthをつけています。
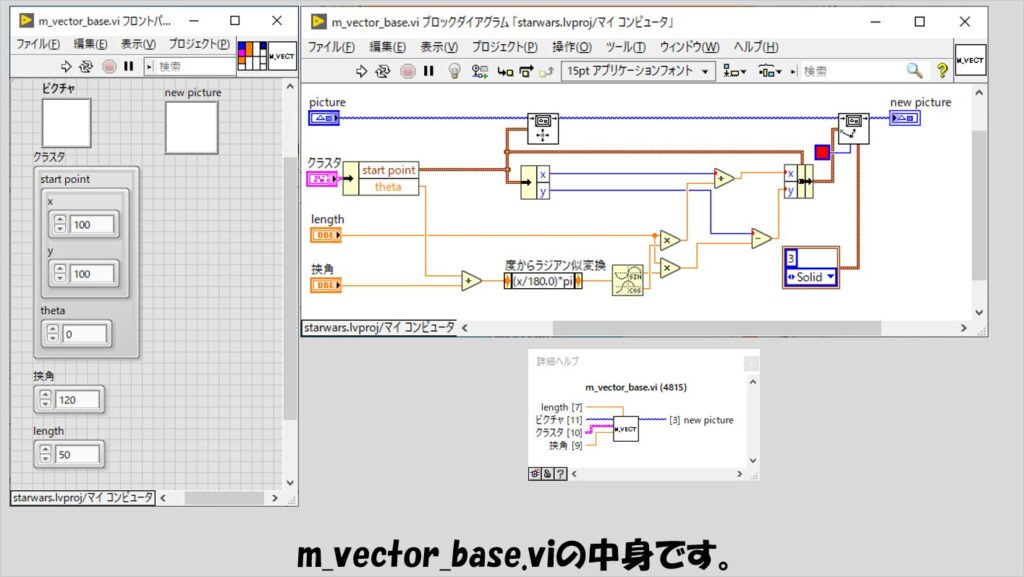
m_vector_base.viも図と同じ理屈です。
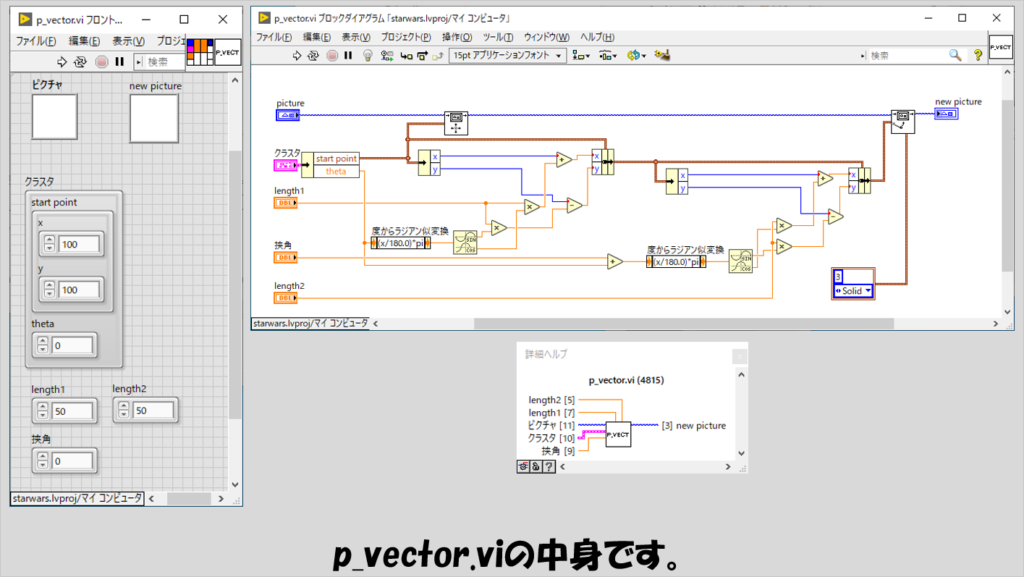
最後にpベクトルについてのサブVI、p_vector.viは以下の通りです。
lベクトルとmベクトルの足し算なので、単純にlベクトルの計算とmベクトルの計算をそのまま行います。
しかし、pベクトルはlベクトルの長さとmベクトルの長さを定数倍する必要があるため、それぞれに異なる長さ係数を掛ける必要があることに注意します。
これらサブviを使ったプログラムで、挟角だったりhやvといったパラメータをいろいろいじって、pベクトルがどのような動きになるかを確認してください。
この調子で、これを2次元平面に落とし込む、つまりhとvの組み合わせで対応する部分のピクチャ上のピクセル値を2次元平面上に1対1対応させるプログラムを作っていきます。
ここは、LabVIEWでピクチャを扱うプログラム自体の難しさがありますが、計算式は今まで説明した通りなので、何となくやっていることは分かるかなと思います。
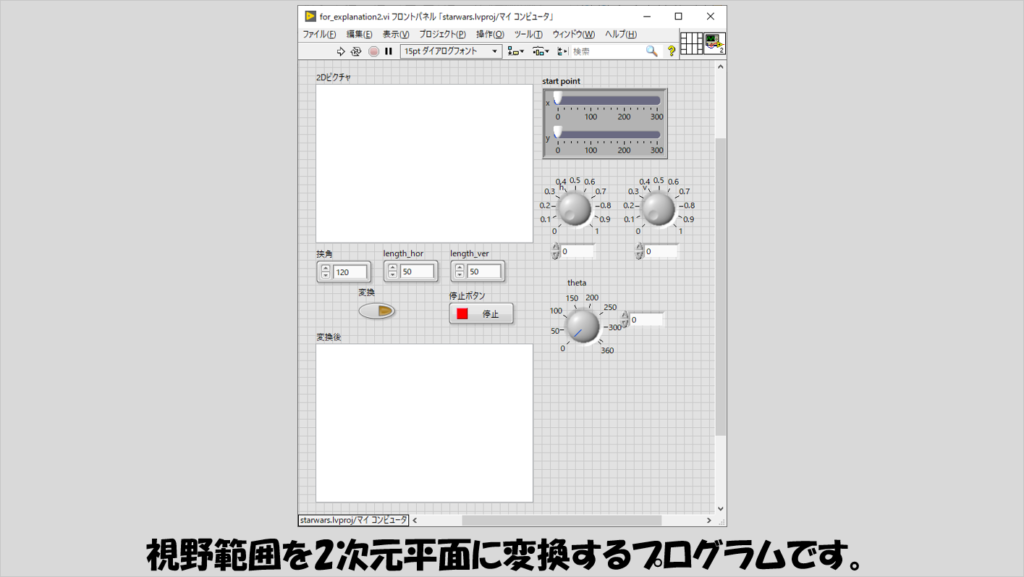
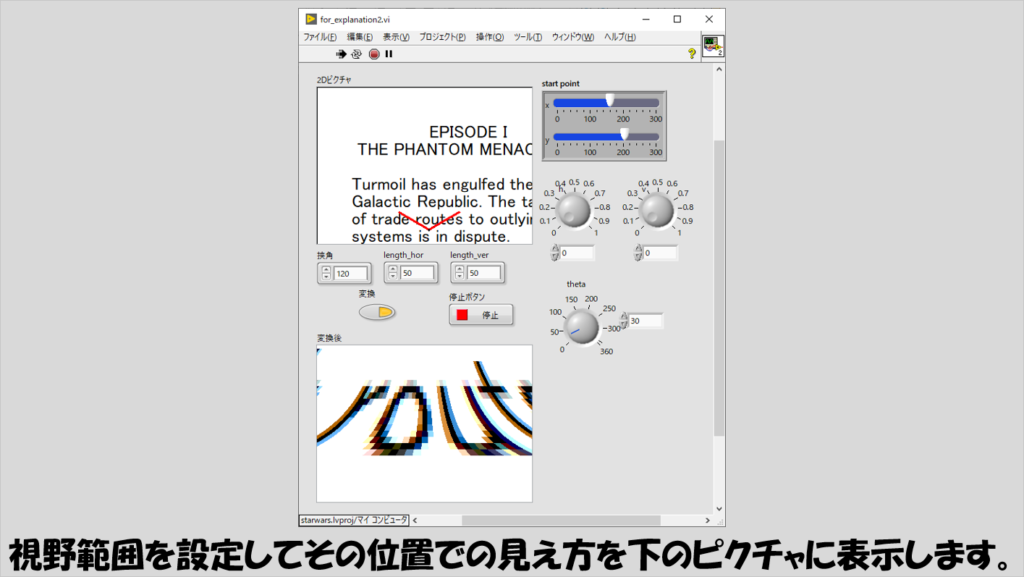
プログラムを実行すると、視野範囲の文字列を変換して別のピクチャに表示できます。
このプログラムのブロックダイアグラムは以下の通りです。
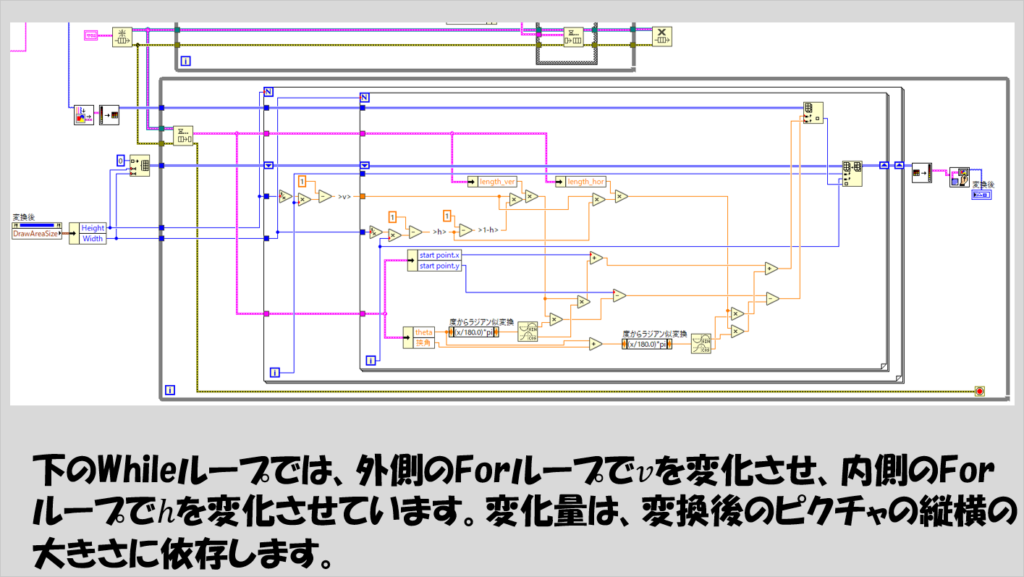
Forループを2重に使用して、外側のForループでvを変えて内側のForループでhを変えています。
変換後のピクチャの描画領域の縦横のサイズはプロパティノードで取得できるので、vやhをこれら縦横のサイズで割ることで、Forループ一回分のvやhの変化量を計算し、これにForループの反復端子の値を掛けることで、vやhを少しずつ変化させるようにしています。
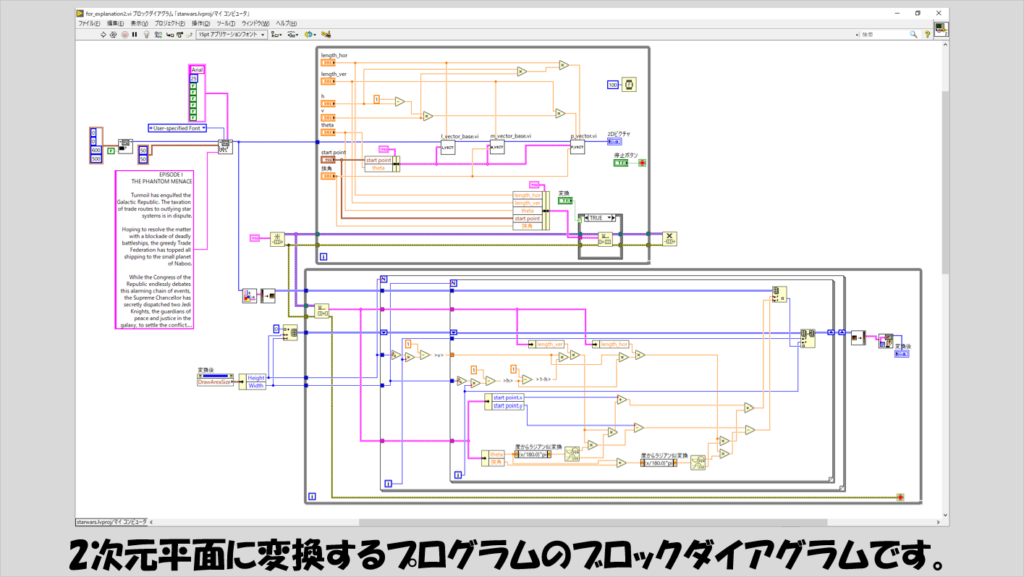
上のWhileループは、先ほど作ったプログラムとほぼ同じで、下のWhileループでの演算に必要なパラメータをキューを使用して渡しています。
下のWhileループでは、hとvをForループの反復端子を使用して離散的に変えています。
上の方で数式で説明した内容を落とし込んでいると考えてください。
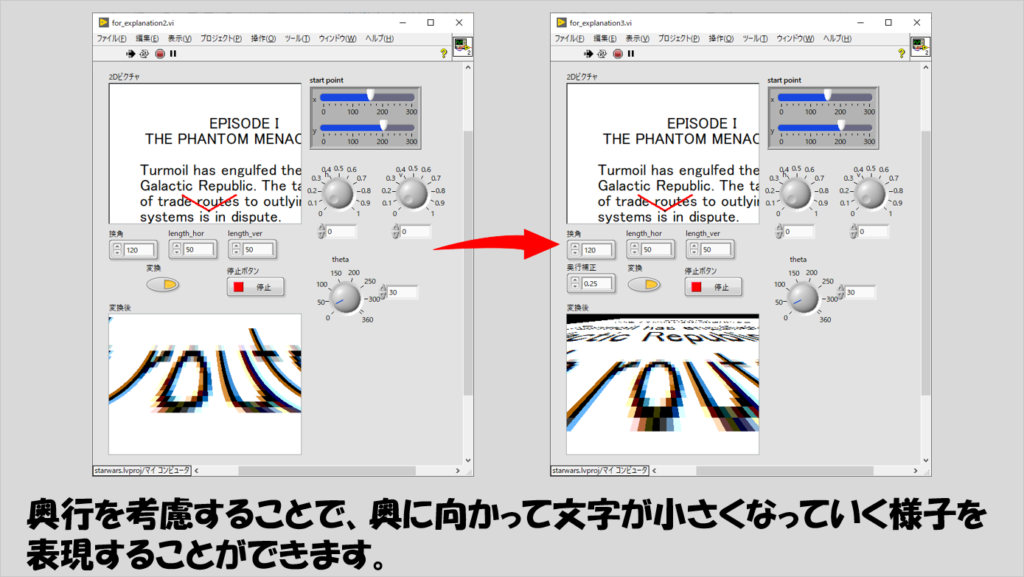
ただし、このプログラムを実行しても、実は最終的に欲しい画像は得られません。
それは、奥行補正をしていないからです。
通常、例えば何か景色を見た時、近くのものは大きく見えて、遠くになるにつれて小さくなる、いわゆる遠近感があるのですが、上で紹介した方法ではこの遠近感を考慮した奥行補正がないため、なんだか「のっぺりした」図が得られることになります。
この奥行きを補正するには、長さ方向のパラメータであるvについて、「遠くになるほど小さくなる」効果を持たせるようにします。
数学的な扱いは様々な処理があると思いますが、今回は双曲線関数を使用します。
奥行補正についてのパラメータをpeとすると、
v’=-pe/(1-v)
が奥行補正項であり、これを先ほどの式のvの代わりに当てはめて、
P=(1-h)v’l+hv’m (v’=-pe/(1-v), 0<h,v<1)
とします。
これで、視野範囲内で見えるものを2次元平面に落とし込む準備が整いました。
上のプログラムでvを使っている部分をv’に変えるだけなので、編集は少しで済みます。
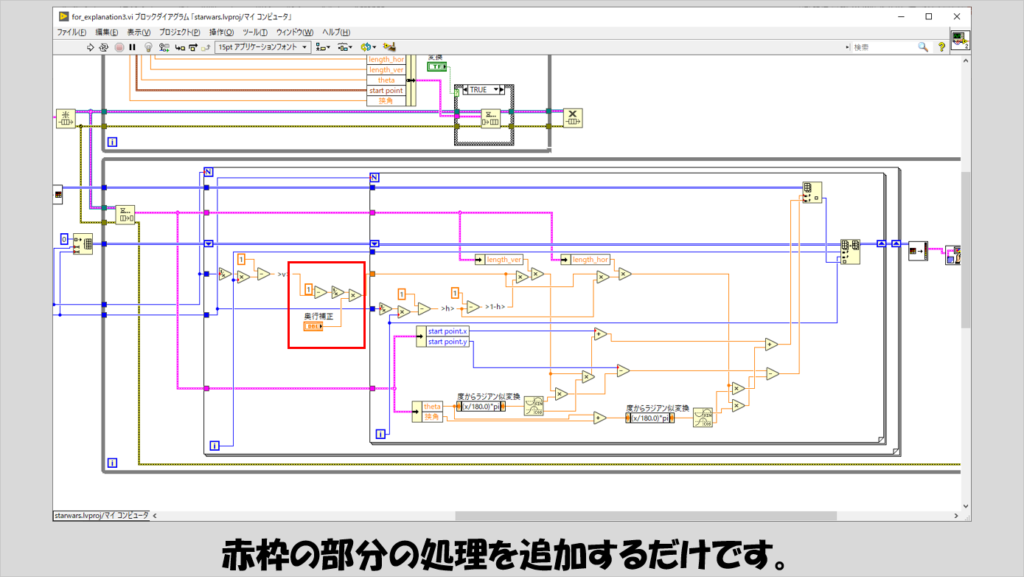
これでプログラムを実行すると、欲しかった画像が得られます。
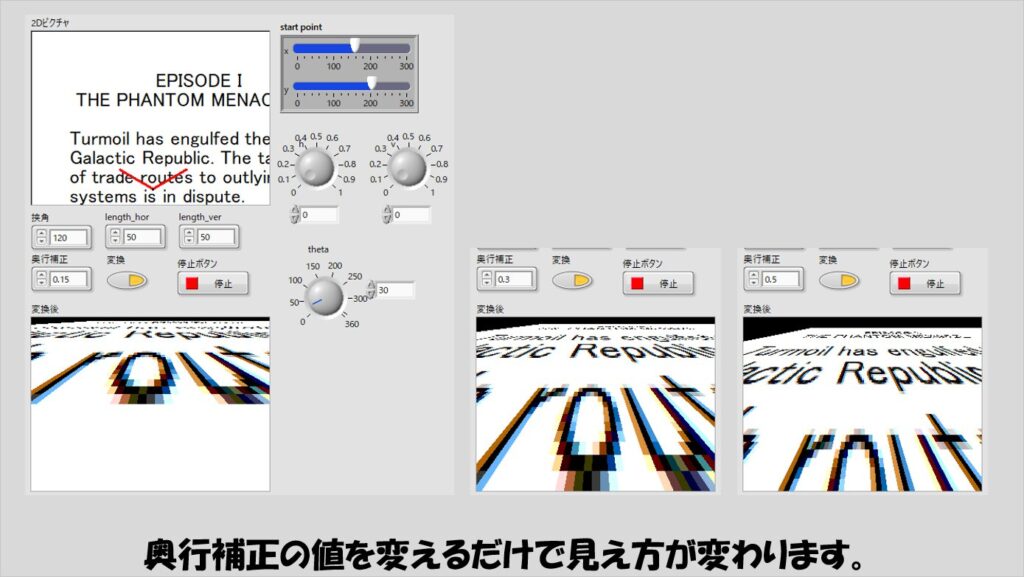
なお、奥行補正の項peは、画像を見ている高さを変えるのに相当します。
peの値が0に近いほど、画面になるべく近づいているような感じがして、値が大きくなると高いところから見下ろしているような画像となります。
あとは、これらの計算が色々とワイヤが煩わしく煩雑なので、フォーミュラノードに「成形」しなおせば目的のプログラムの完成です。
これまでの説明の内容は高校数学までの数学で習う、三角関数なりベクトルなりを用いた計算が途中で入っていただけに、複雑と思われたかもしれません。
ただ、こういった処理は、いったん数学的な理屈は完全に理解できていないまでも、プログラムで実装して、色々パラメータを動かすことで「こういう動きになるんだ」ということを実感することによって少しでも理解できるようになればそれでいいのかなと思います。
あまり難しく考えず、こういうことを考えればこんなことができるんだ、と気楽に思ってもらえればと思います。
本記事では、スターウォーズのように流れる文字を作成する方法を紹介しました。
元々文字は2次元だったのを流れるように見せる、つまり奥行きの感覚を追加するということで、これは2次元を疑似3次元に変換した形となります。
別の記事で、この疑似3次元についてもう一つ面白い例を紹介したいと思います。
ここまで読んでいただきありがとうございました。

コメント