この記事では、LabVIEWで様々なソートアルゴリズムを実装する方法を紹介します。
効率的かどうかはともかくとして、世の中にある様々なソートのための仕組みをLabVIEWでどう表現するかの一例を紹介しているだけなので、実用性は必ずしも求めていないです。
ただ、ソートされていく様をグラフ表示器などに表すと、各アルゴリズムの「クセ」が可視化されて興味深かったりするので、ぜひ実際に組んで確かめてもらえればと思います。
標準関数でも十分早い
最初に一つ断りを入れておきますが、LabVIEWには標準関数(関数パレットに最初から入っている関数)として1Dソートの関数があります。
そして、この1Dソートはソートー早いです。
この標準関数の1Dソートがどのようなソートアルゴリズムで動いているのか、公式のヘルプドキュメントなどで探しても見つからないのですが、下記のディスカッションフォーラムを信じると、randomized quicksortのようです。

そして、今回の記事で紹介するどのアルゴリズムよりも基本的に早いようです。
なので、今回の記事で紹介しているのは、「標準関数よりも早いアルゴリズムを実装しよう」という趣旨ではなく、あくまで様々なアルゴリズムがどのように動作するかを可視化してみよう、という趣味要素が強いことはまずご了承ください。
扱うソートアルゴリズム
では、本記事で扱っていくソートアルゴリズムについて紹介します。
- ・バブルソート
- ・シェイカーソート
- ・コームソート
- ・挿入ソート
- ・シェルソート
- ・選択ソート
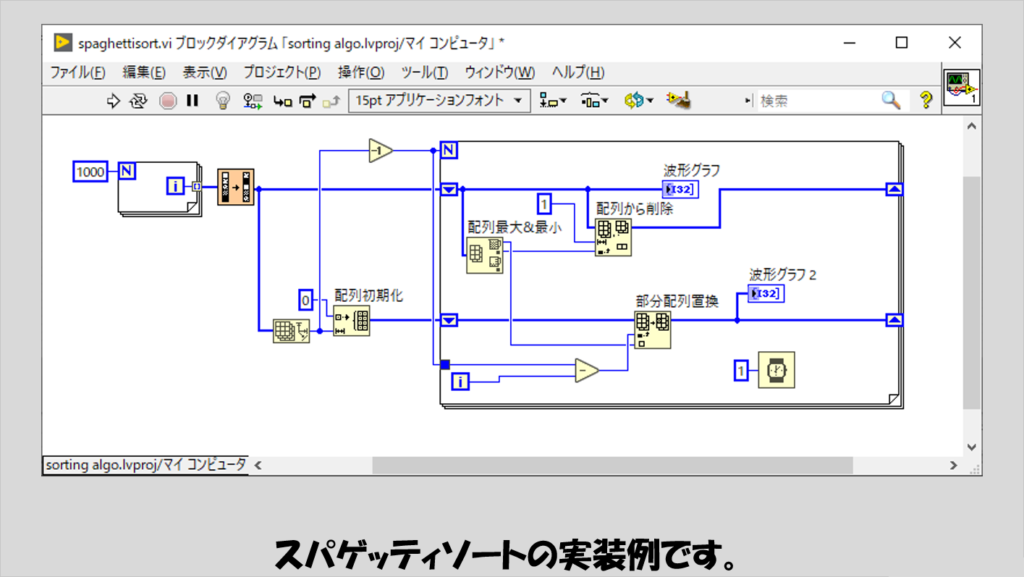
- ・スパゲッティソート
世の中には他にもたくさんのソートアルゴリズムがありますが、実装が比較的単純なこれらを扱っていきます。
記事文面ではプログラム実行時に数値がソートされていく様子を表現することはできないですが、実際に組んでみて、各ソートアルゴリズムがどのように走っていくか、グラフで可視化していくとそれぞれで全然異なる過程でソートされていく様が見えるのでなかなか興味深いです。
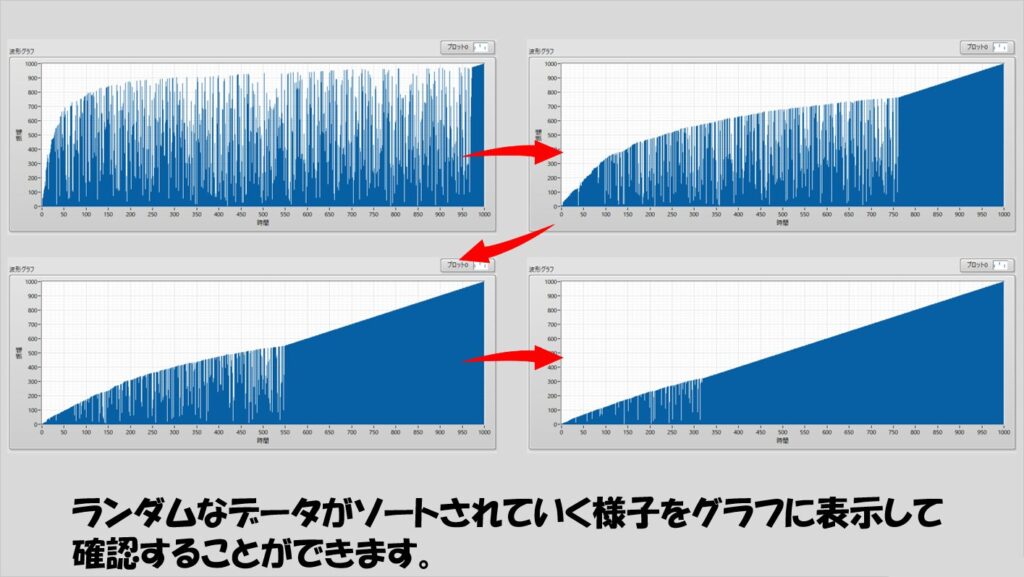
なお、私はアルゴリズムを専門に研究しているわけでもなく正しい実装かどうかは疑わしい点がありますのでご注意ください(実行結果だけ見ればどれも最終的にはソートできることは確認済みです)。
また、ソートは数値配列を対象とし、「小さい値からだんだん大きい値になる」ようないわゆる昇順に並び替えていくことを前提とします。
バブルソート
ものとしてはかなりオーソドックスな部類に入ると思います。
ソート対象の配列の要素を小さい方から順番に調べ、隣同士大小が逆であればそれを入れ替える、という操作を最終的に全体がソートされるまでひたすら繰り返します。
繰り返す際は、再び対象配列の要素の小さい方から順に調べていきます。
なお、以降で紹介する他のプログラムでもそうですが、プログラムの最初では配列をシャッフルする動作を入れて、ソートアルゴリズムを実装しているループには待機関数を入れていますが、本来最速でソートしたい場合にはもちろん待機関数は必要ありません。
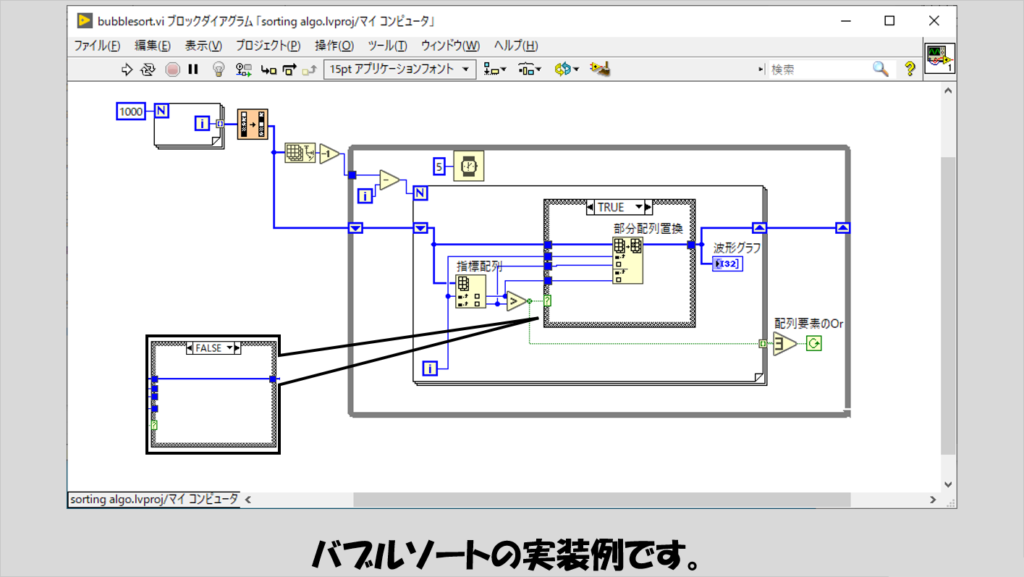
シェイカーソート
こちらはバブルソートからの派生形です。
シェイカーソートでは、一度対象配列の要素の小さい方から調べた(ここまではバブルソートと同じ)後に、今度は要素の大きい方から小さい方に向かって調べ、今度はまた要素の小さい方から調べて、ということを繰り返します。
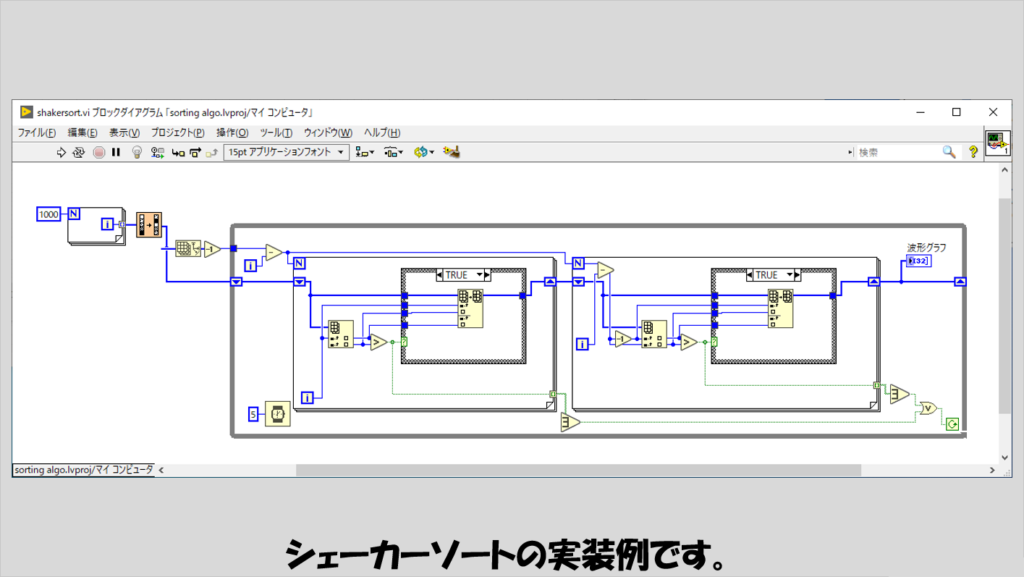
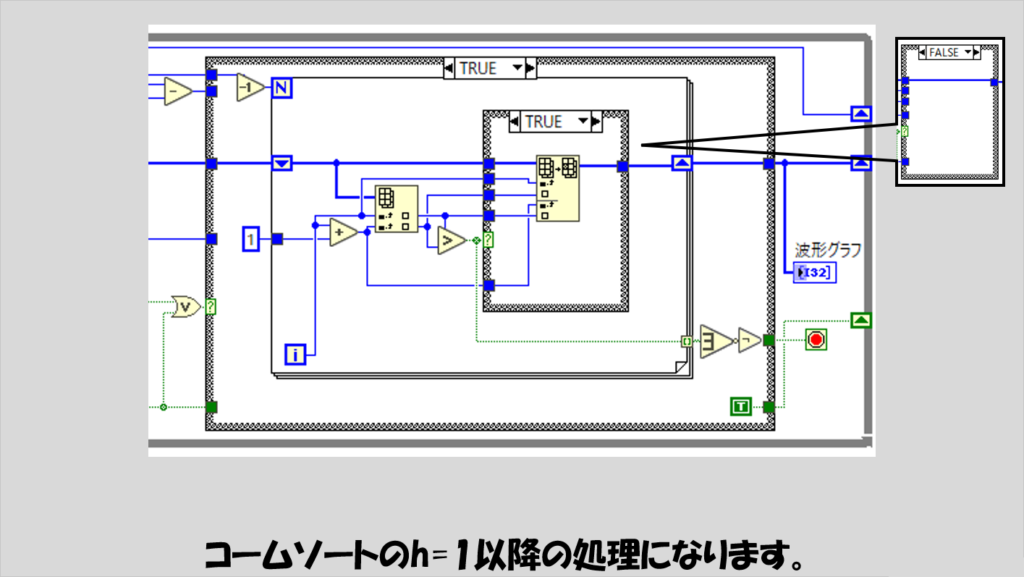
コームソート
少し処理が複雑になったバブルソート、といった感じのアルゴリズムです。
手順としては、まず対象配列の総数(サイズ)を1.3で割った商(小数点以下切り捨て)を間隔値hとして定義します。
そして、対象配列の要素番号iと要素番号i+hとの大小関係を比べるという操作をi=0からi+hが配列サイズを超えるまで繰り返します。
これが終わったら今度はhを1.3で割った商を新しいhとみなし、同じく要素番号iと要素番号i+hの大小関係を比べる、という操作を繰り返します。
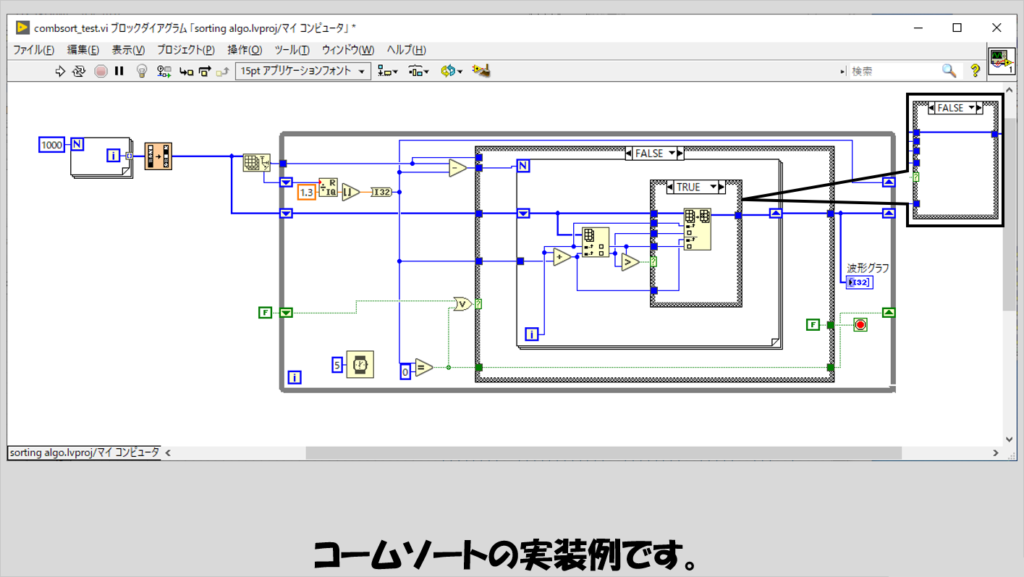
この一連の繰り返しをhが1になったあとは、残りの要素で順番が違っている要素がなくなるまで処理を繰り返していきます。
挿入ソート
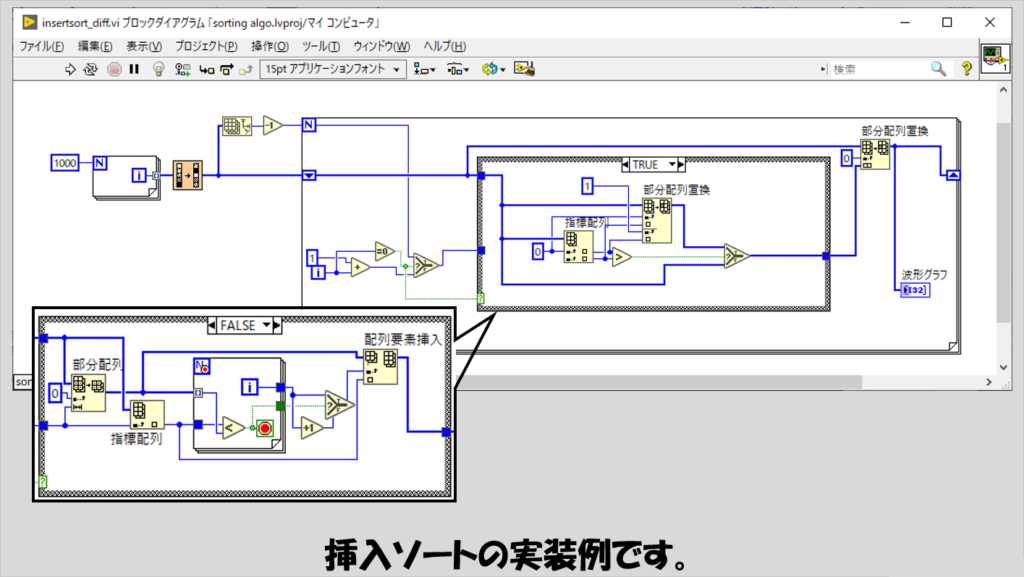
要素を正しい位置に挿入することでソートさせていくアルゴリズムです。
一番最初だけ、順番の大小単純に比べて逆なら入れ替える、という操作になりますが、これ以降は一つ一つの要素を毎回それまでの要素と合わせて昇順になるように調べていきます。
なので、ソートされていく様を見ると、端からどんどんソート済みの結果が左から右へ流れていくような様子がみてとれます。
シェルソート
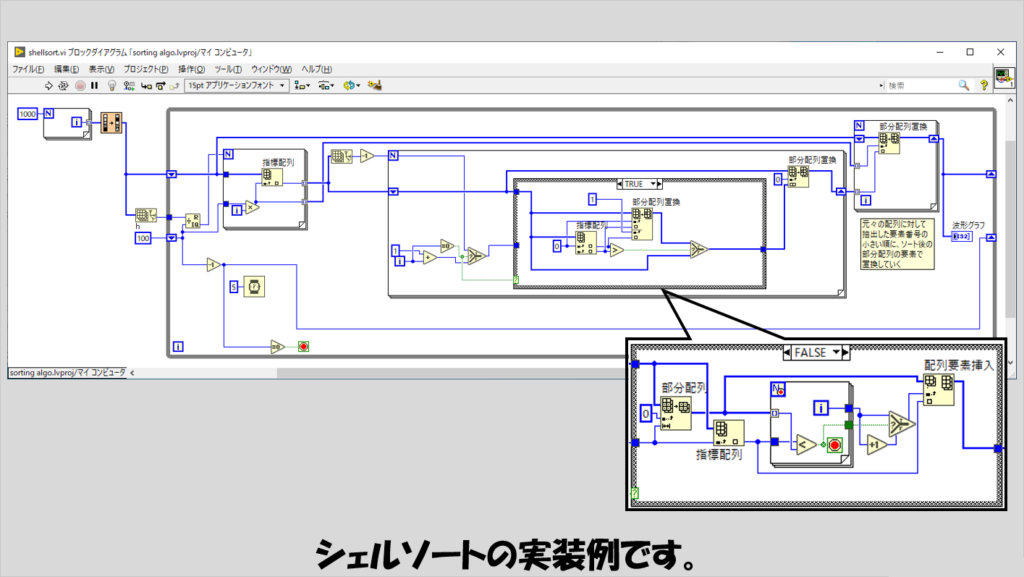
挿入ソートの応用のようなアルゴリズムで、今回の記事で紹介しているソートの種類としては早い部類になります。
適当な間隔値としてhを定め、この間隔hごとにとびとびの要素番号の要素をソート対象配列から取り出し、これらに対して挿入ソートを適用します。
こうして「一部分」に対してソートを行ったら、今度は間隔hを狭めて同じことを繰り返し、最終的にh=1になったあとの挿入ソートで終了します。
実装上、間隔hごとのとびとびの要素を取得した「部分配列」に対し挿入ソートを適用後、これを元の配列に戻す操作をいれており、戻す際に元々取り出していた要素番号の場所に部分配列の要素番号が小さい方から戻す操作をしています。
間隔hの決め方について、より良いhを決める方法はいくつかあるようですが、最適解は見つかっていないようです。
hを狭める方法は今回は単純に1ずつ減らすような実装をしていますが、こちらについても最適な減らし方があるかもしれません。
選択ソート
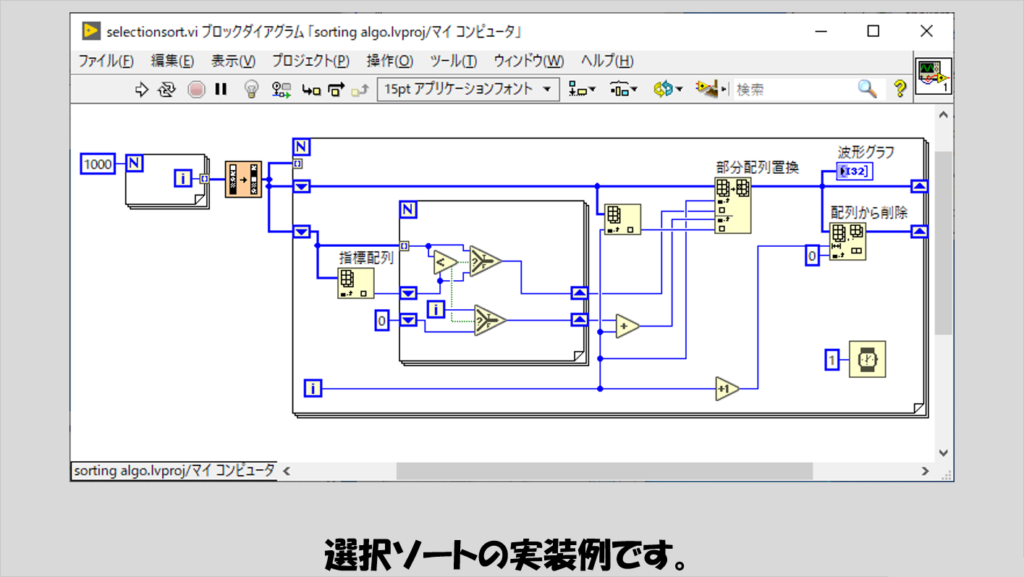
こちらは、ソート対象配列の要素番号が小さい方から、「残りの配列」の中で一番値が小さい値を取り出して置換する、という操作を行っていきます。
残りの配列の中で最小の値を決めるのに、「配列最大最小」の関数を使用するという手はありますが、今回はあえてループ処理で毎回最小値を探しています。
スパゲッティソート
こちらはソート対象の配列の全体から最大値となる要素を取り出し、次に残った配列からまた最大値となる要素を取り出し、という操作を繰り返します。
今回は配列最大最小の関数を使用してシンプルに書いています。
名前の由来は、Wikipediaによると「乾燥スパゲティを長さ順に並べ替える手順に例え」てこのソートの説明がなされたから、とのことです。
「1D配列ソート」が最適?
上で紹介した各アルゴリズムそれぞれに特徴があり、ソートできる速さも様々だったということを踏まえて、標準関数である1D配列ソートを使用すると、その速さが際立ちます。
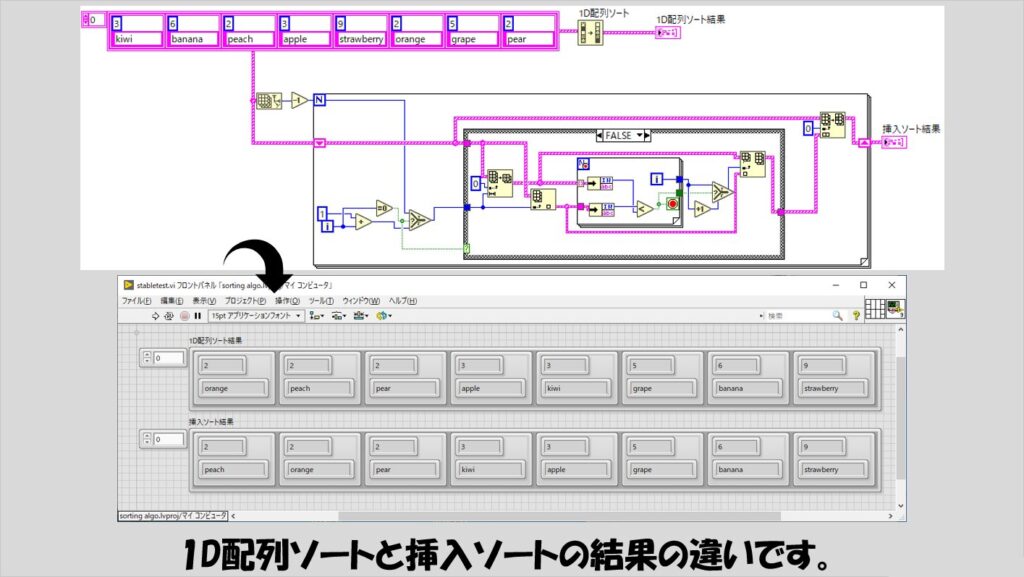
ただし、この1D配列ソートで実装されている(と思われる)randomized quicksortの元になっているクイックソートは、「安定ソート」ではないのに対し、今回の記事で紹介したもののいくつかは安定ソートとなっています。
安定ソートとは重複する要素があった場合に、それらの前後関係がソート後にも保たれているようなソートを指します(wikipediaの説明がわかりやすいと思います)。
今回の記事で紹介したソートで安定ソートなのは、バブルソート、シェーカーソート、挿入ソートが該当します。(シェルソートは挿入ソートの派生ですが、一部の値をピックアップする処理が入るため安定ではなくなります)
以下の図では1D配列ソートと挿入ソートアルゴリズムを実行していますが、結果の順番が同じではないことがわかると思います(挿入ソートの結果は、入力時の配列の例えばpeachとorangeの前後関係が出力時にも保たれています)。
これら様々なソートの種類や実行の様子を見ると、やはりアルゴリズムというのはとても大事だなと思います。
計算の実行速度や実行時のループの回数など、種類によって大きく尾となっていることがわかりましたが、標準関数で実行すると一瞬で終わるので、普段は有難く標準関数でソートさせてもらいましょう。
ここまで読んでいただきありがとうございました。
コメント