二曲線の交点を求める

この記事で扱っていること

• グラフの交点座標を求める方法

を紹介しています。

注意：すべてのエラーを確認しているわけではないので、記事の内容を実装する際には自己責任でお願いします。また、エラー配線は適当な部分があるので適宜修正してください。

LabVIEWでは、（数値）データを表わす方法として、波形グラフと波形チャート以外にXYグラフというものがあります。

同じ「グラフ」とついているので波形グラフとほとんど性質は同じなのですが、波形グラフは入力された配列の要素番号がX軸の値に強制されるのに対し、XYグラフはX軸の値も指定できるという点で異なります。

二つの曲線をグラフ上に表す際に、この曲線に交点があったとしても、波形グラフでは交点のX値が整数でないと表わせませんが、XYグラフでは整数値以外のX値でも表すことができます。

そこで、二つの曲線でいくつか交点がある場合にそれらの交点のX座標およびY座標を求めるプログラムを作ってみました。

どんな結果になるか

プログラムで指定するのは、求める交点の細かさ、です。二つの曲線の交点が整数値ではないXの値を持つ場合、そのXの値を求めるのにどれくらいの精度とするかという指定で、要は小数点以下何桁まで表したいか、になります。

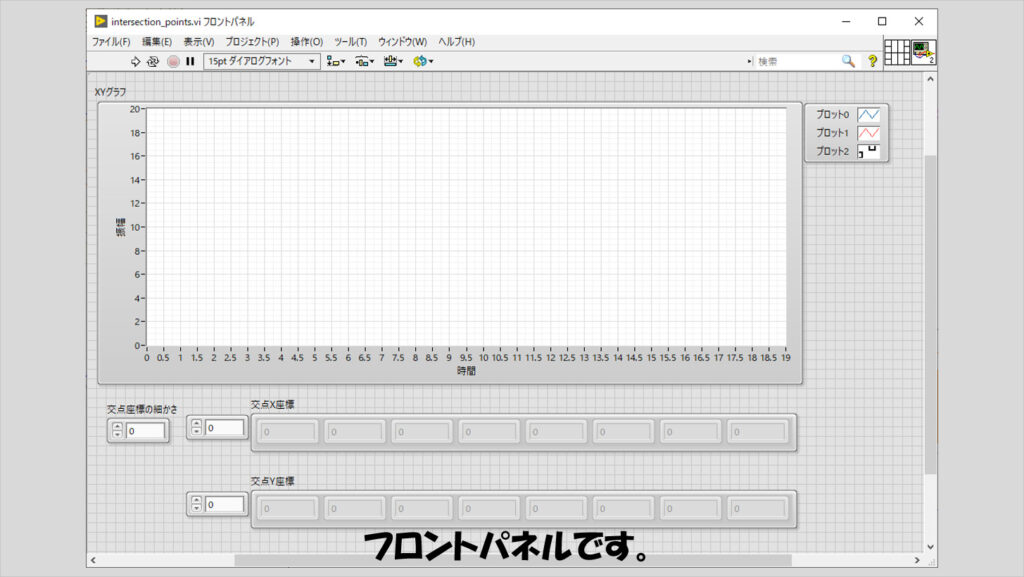
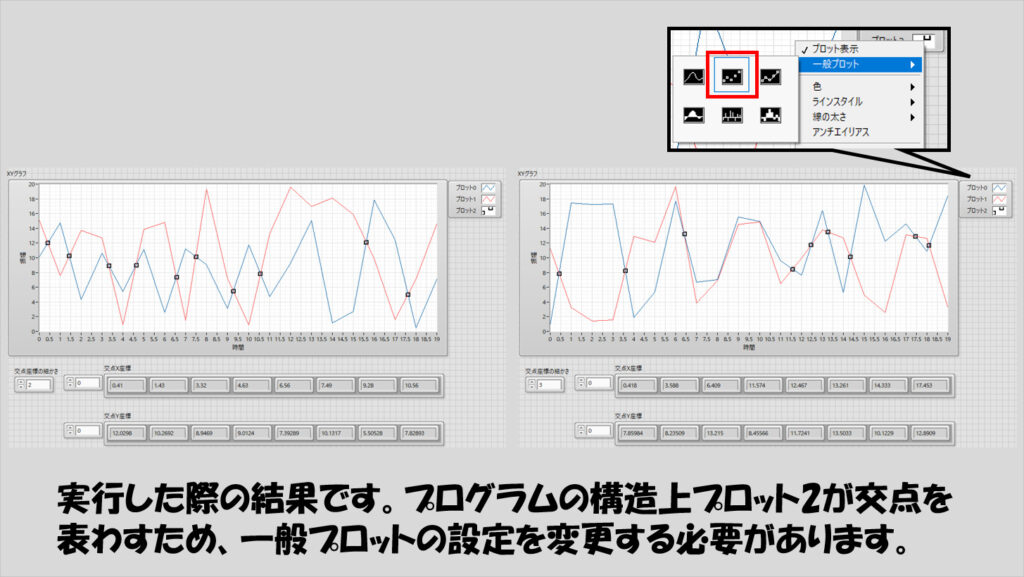
試しに乱数データを用いて交点を求めるようにしてみました。プロットは2つの曲線を表わす以外に交点部分に印をつけており、この印は3番目のプロット（プロット2）を使用しています。

デフォルトの設定だとプロットは線で結んでしまうので、一般プロットの設定で線を表示せず点で表示するようにしています。

プログラムの構造

ブロックダイアグラムは少し複雑かもしれません。ただ、やっていることはそこまで難しいことをしていません。

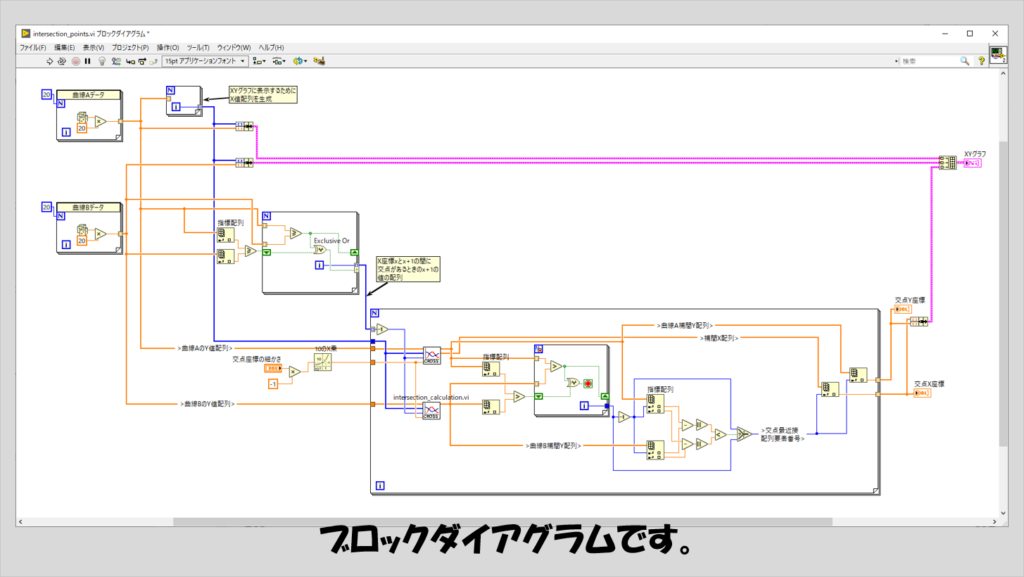
二つの曲線のデータ（1次元配列）を使って、まずは交点がどの位置にあるか、大まかな位置を特定しています。そのために、二つの曲線が交わるとはどういうことか考えます。

例えば曲線Aに点(1,2)、曲線Bに点(1,5)があったとすると、この時点では曲線Bの点の方が曲線Aの点よりも上に来ていることになります。これらの一つとなりの点（X=2の点）について、もし曲線Aが(2,3)という点を持つとき、交わるための条件は「曲線BのX=2の点のY座標が、3よりも小さい」、言い換えればX=2のときに曲線Aの点が曲線Bの点より上になっていればいいわけです。

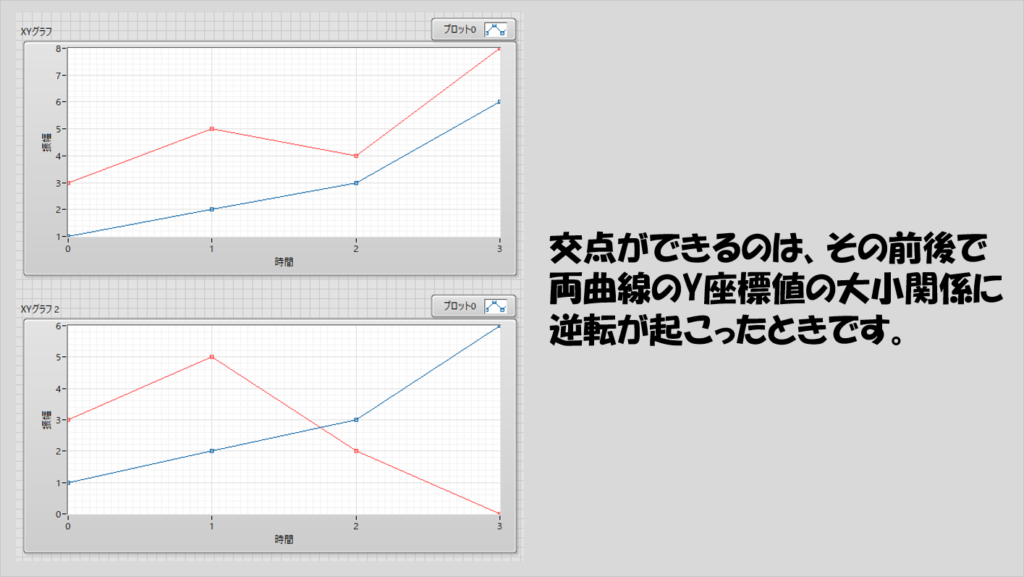
実際は逆でも良く、「あるXのときに曲線Aの点が曲線Bの点より上に来ていたとして、X+1のときに曲線Aの点が曲線Bの点よりも下に来る」場合も交わりが発生します。

これらをどう検出するかについてという観点で考えると、「あるXの時の曲線A、曲線Bの上下関係が、X+1で逆転していればいい」ということになります。

なので、常に曲線Aと曲線Bの大小関係を調べて結果をブール値で得て、その次の点でブールが逆転すれば交点がある（TRUE）、逆転していなければ交点がない（FALSE）と判断できます。

二つの曲線でそれぞれのXのときの大小関係を調べるのは自動指標付けを有効にしたForループが便利で、あるX座標（N回目のループ）での「曲線AのY座標 > 曲線BのY座標」のブールの結果と次のX座標（N+1回目のループ）での「曲線AのY座標 > 曲線BのY座標」のブールの結果が

• N回目ループでTRUE、N+1回目ループでFALSE
• N回目ループでFALSE、N+1回目ループでTRUE

の場合だけ交点があるとしてTRUE、上記以外の条件ではFALSEと判定する必要があります。これは、排他的論理和（XOR）によって判別できます。

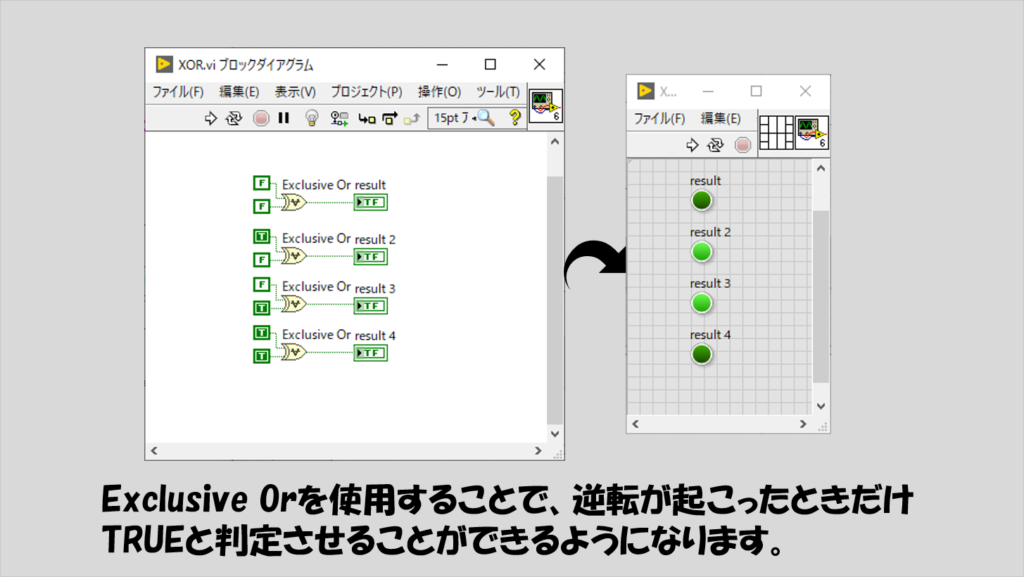
この考えを使って、交点を挟むX座標を求めます。ただし、この方法ではForループの中で使用するシフトレジスタの初期値を各曲線の最初の値どうしの大小関係で先に求めてしまいます。その値をシフトレジスタの初期化に使用すると、Forループ内の一番最初の不等号の結果と必ず一致（FALSEどうし、あるいはTRUEどうし）となるので、交点と判定されることはなくなります。

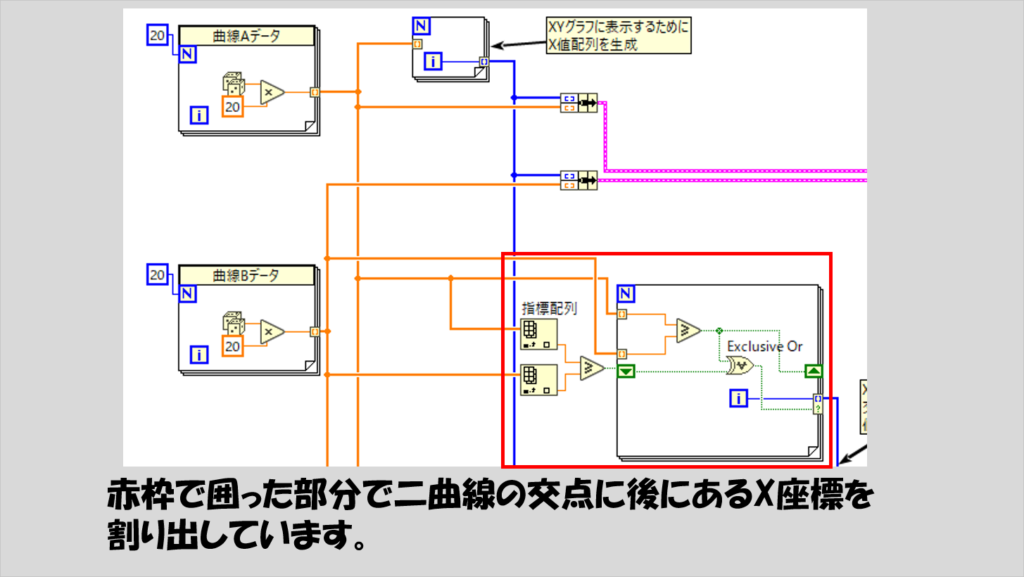
交点の位置がわかったら、あとは各交点に対して、それぞれの曲線でこの交点付近に対し補間をかけて、また同じ理屈でさらに細かく交点を求めていきます。

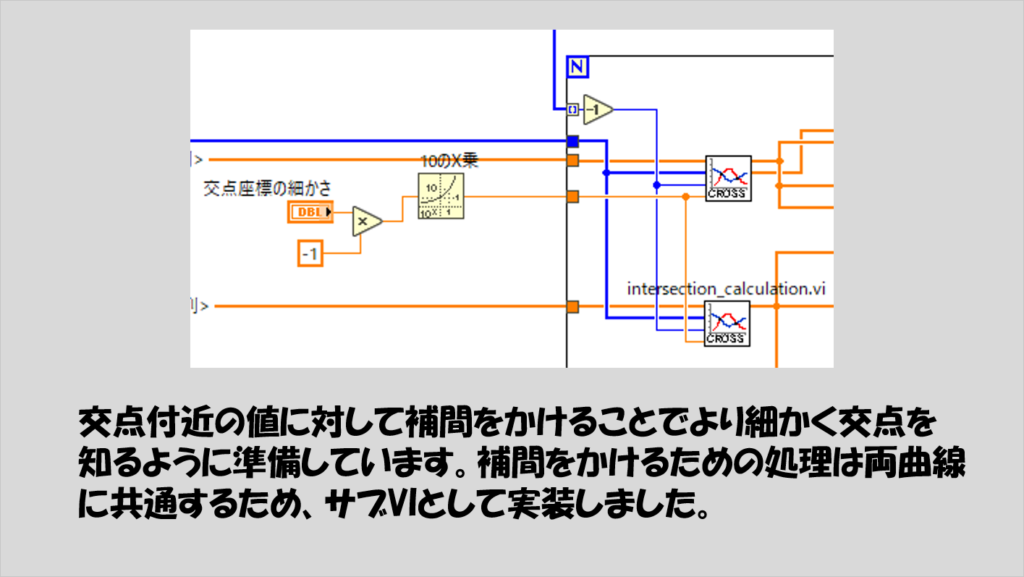
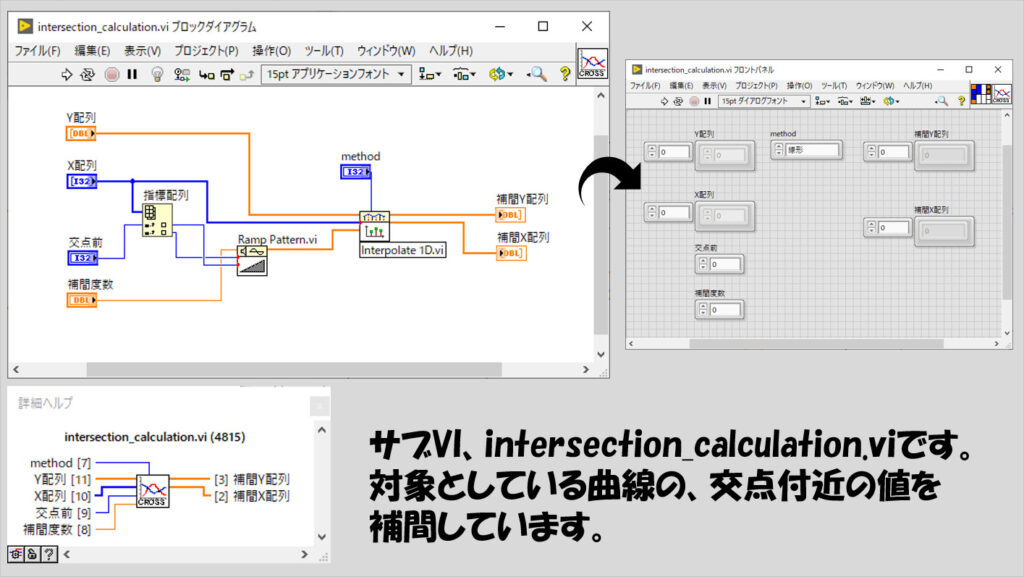
補間をかける部分は曲線により差があるわけではないので、サブVI、intersection_calculation.viにして両方の曲線に対して適用しています。

なお、今回はとりあえず線形補間にしていますが、サブVI内で使用している1D補間.viは線形補間以外の補間方法も選ぶことができます。

補間の刻みを細かくするほど本来の交点に近づきますが、真の交点を補間値で表せていない場合には、交点がある直前、直後のX座標における、曲線Aと曲線BのY座標の差の絶対値をそれぞれ計算し、より差が小さいほうが交点に近いと判断しています。

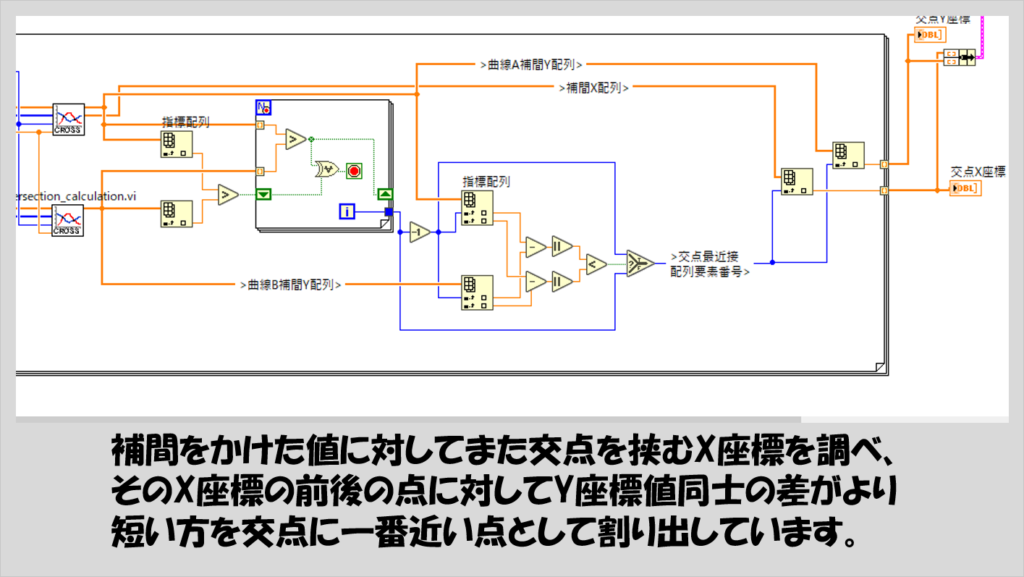
これで交点を求めるプログラムが完成します。

数式から導く

さて、上で紹介したプログラムでは、交点付近のデータについて補間をかけた状態で、一番交点に近いX軸値を求めるという方法をとっていました。

が、交点を挟んだ前後2点を線形補間するのでいいのであれば、2つの曲線の中のある範囲の線分二つの交点を計算で求めることもできるはずですね。

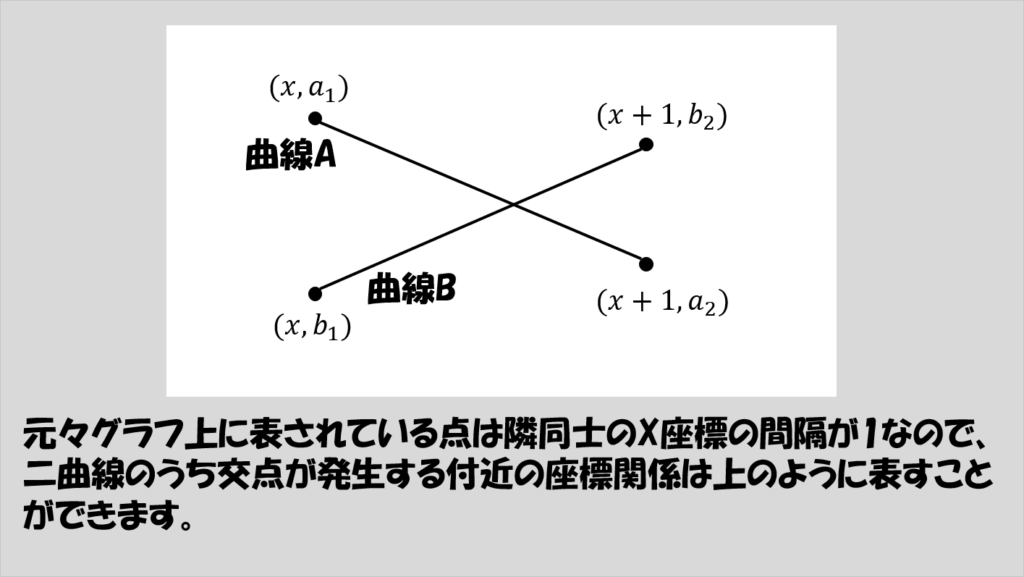
詳しい計算は特に難しいことはないと思うので結果だけ書くと、

|a2 – a1| = |b2 – b1|のとき、交点の座標は(x + 1 / 2, (a2 – a1) / 2)

|a2 – a1| ≠ |b2 – b1|のとき、交点の座標は(x + 1 – (a2 – b2) / M, -(a2 – a1) * (a2 – b2) / M + a2)

(ただしM = (a1 – a1) – (b2 – b1))

となります。

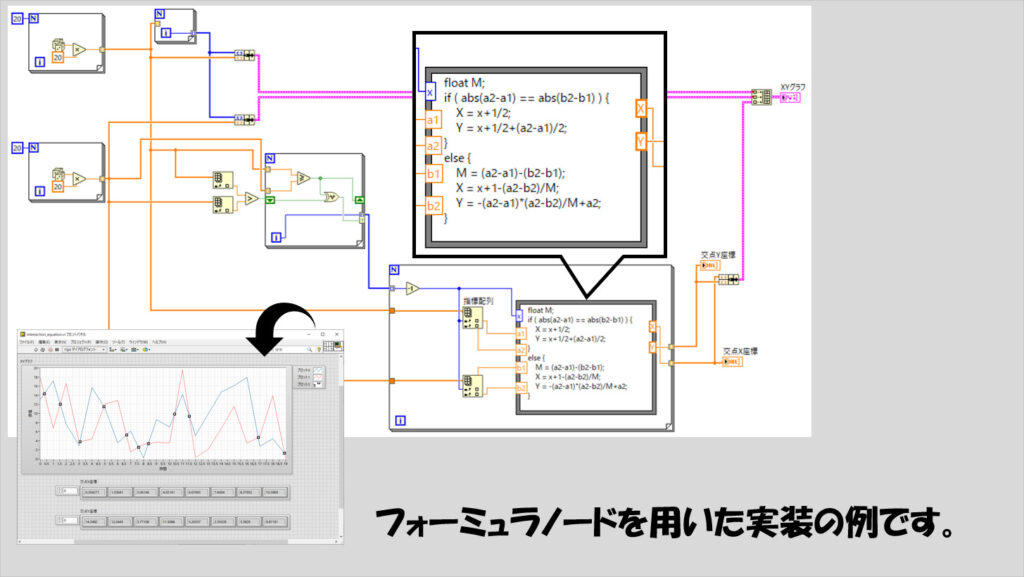
あとはこれをLabVIEWの数式ノードで表すだけですね。数式ノードの計算は例えば以下のような式でよさそうです。

実装はこちらの方がよりシンプルです。

ただし、補間は線形補間に限られます。他の補間方法が必要、という場合には（究極的には数式でできなくもないとは思いますが）最初に紹介したプログラム的に交点の近似値を求める方法での実装を考えることになります。

この記事では、二つの曲線の交点を求めるプログラムを紹介しました。

大雑把に交点の位置を特定してから値を補間して求める方法と、フォーミュラノードを使用して求める方法になっています。フォーミュラノードの方が実装がシンプルですが、これは交点を求めるのが線形補間である前提となっています。一方で最初に紹介した方は線形補間以外の補間方法もとれるので、場合によってはこちらが便利かもしれません。

参考にして頂けたらうれしいです。

ここまで読んでいただきありがとうございました。