この記事では、LabVIEWで再帰処理を行う際の設定とその使用例を紹介しています。
テキスト系のプログラミング言語でも「ある関数の引数にその関数自身を指定する」といった書き方をすることで実装ができる再帰処理は、LabVIEWでもある設定さえしてしまえば実装できます。
再帰的なプログラムを書かないと処理できないようなこともある一方で、場合によっては工夫が必要になることもあるので、そのあたりの例も簡単にですが紹介しています。
再帰処理とは
まずそもそも再帰処理とは何なのか、ということから入っていきます。
既に知っているよ、LabVIEWでのやり方を知りたいんだ、ということであればこの章は飛ばしてもらって大丈夫です。
LabVIEWに限りませんが、プログラミング言語では再帰処理という特殊(?)な処理を実装することがあります。
再帰とは、読んで字のごとく、「再び帰ってくる」といった状態のことで、プログラムにおける実装内容としては入れ子の構造で処理を行い、「もうこれ以上入れ子にならない」状態になるまで進み、それが終わったら、今までの処理内容に戻って(帰って)くるような工程を指します。
・・・言葉だけではうまく伝わらないですね。
実例を見るのがわかりやすいと思うので、よく例として取り上げられるフィボナッチ数列の例を元に再帰処理の内容について紹介していきます。
フィボナッチ数列を知らない方もいるかなと思いますので、まずはどのような数列なのかということを示すと、以下のような数の並びを指します。
1,1,2,3,5,8,13,21,34,55,89,144,・・・
この数の並びはある法則をもって並んでいます。それは、「N番目の数は、N-1番目の数とN-2番目の数の和」という法則です。
この場合、N = 1やN = 2についてはあらかじめ決めておく必要がありますが、今回はN = 1もN = 2も「1」としています。
※N = 0から始めるべき、といった考えもあるかと思いますが、数学的に厳密な定義は置いておいて、フィボナッチ数列の作り方に焦点を当てて考えています。
高校の数学で習う表現でいえば、N番目の数をa_(N)と表すことにすると、「N番目の数は、N-1番目の数とN-2番目の数の和」とは
a_(N) = a_(N-1) + a_(N-2)
と書くことができますね。(数式が苦手な方はごめんなさい。あくまでイメージをつかめればOKです)

これがなぜ再帰処理と結びついているかを見るために、まずは簡単にNに具体的な数を入れて確認してみます。
N = 3を考えると、上の式にN=3を代入して
a_(3) = a_(2) + a_(1)
という計算になります。
今、N = 1もN = 2も値がわかっている(両方とも1としている)ので、このa_(3)は計算することができて、a_(3) = 2となります。
次に、N = 4の場合を計算してみることを考えます。
a_(4) = a_(3) + a_(2)
この計算、N = 3の結果が必要になっています。今回は既に計算をしてa_(3) = 2とわかっているので、a_(4)も計算できますが、これを別の書き方をすると次のようになるはずです。
a_(4) = {a_(2) + a_(1)} + a_(2)
何のことはない、a_(3) = a_(2) + a_(1)という式をa_(4)の計算式に当てはめただけです。
ここで改めて注目すべきは、a_(4)という計算をするためにa_(3)を使用し、このa_(3)はa_(4)の計算と「構造は同じだが代入した値が異なる計算」をして得られていた結果だった、ということです。

慣れてきたところでもう少し一般化するために、上ではNに具体的な数を入れて計算しましたがN = nとして計算式を書くことにします。
すると、a_(n) = a_(n-1) + a_(n-2)の式が
a_(n) = {a_(n-2) + a_(n-3)} + {a_(n-3) a_(n-4)}
と書き換えることができますね。
そして、もうお気づきの方もいると思いますが、この書き替えた式は(nが大きければ)まだまだ書き換えることができます。
a_(n) = [{a_(n-3) + a_(n-4)} + {a_(n-4) + a_(n-5)}] + [{a_(n-4) + a_(n-5)} + {a_(n-5) + a_(n-6)}]

Nが大きいと、どんどん書き換えを行うことができ、どこまで書き換えられるかというと、最終的にa_(1)とa_(2)しか使われていない足し算になるまで書き換えることができるのが想像つくかなと思います。
最終的にもう入れ子にならない状態にたどり着いたら、a_(1)やa_(2)は値がわかっているので計算をすることができます。

違う言い方をすれば、最終的なa_(1)やa_(2)だけの式の一つ前はa_(3)があったはずで、その前はa_(4)があったはず、というように、さかのぼるほどNが大きな数の計算を行っていたはずで、この調子でプロセスを逆にたどっていくことで、元々の処理(a_(N)の計算)の結果を得ることができます。
この様子を敢えて図で書くとこんな感じになります。
N回目の処理の結果を求めるには、その下の階層であるN-1回目の処理の結果が必要であり、このN-1回目の処理の結果を求めるにはN-2回目の処理の結果が必要であり、といった具合にどんどん奥深くに入っていき、最終的に1回目(=それだけで処理が完了できる)の処理の結果にたどり着きます。
そして、1回目の結果がわかったらそこから2回目の結果がわかり、これにより3回目の結果がわかり、とどんどん来た道を戻っていき、N-1回目の結果をもとにN回目の結果がわかる、ということになります。
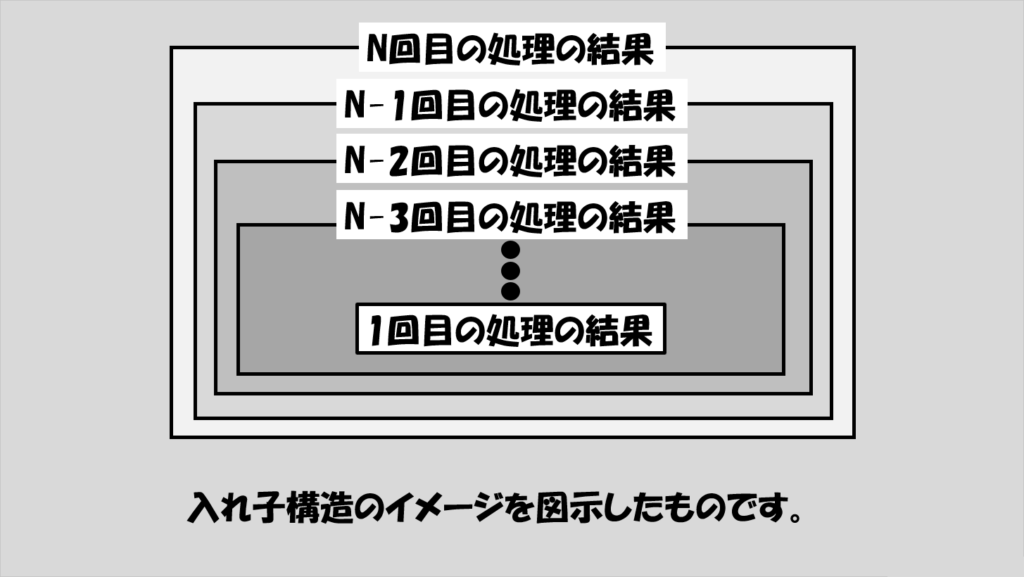
このような、入れ子の構造で処理を行い、「もうこれ以上入れ子にならない」状態になるまで進み、それが終わったら、今までの処理内容に戻って(帰って)くるような工程を経る、これが再帰処理です。
この性質上、再帰処理はいわゆる高校の数学で習う数列の漸化式のような処理を行うのに相性がいいとされます。
例として挙げたのは、再帰の様子を数で表すのに都合がいいフィボナッチ数でしたが、実際は題材を数(計算)にしなくてもいいわけで、例えば図形的に再帰処理を行えば、面白い図形が書けます。
一例として、「一つの辺に三角形を一つ書く」ことを再帰的に繰り返すことで描かれるコッホ曲線を再帰の考え方を用いてLabVIEWで書くと次のような感じになります。(本記事でこの図形の書き方は扱いませんが)
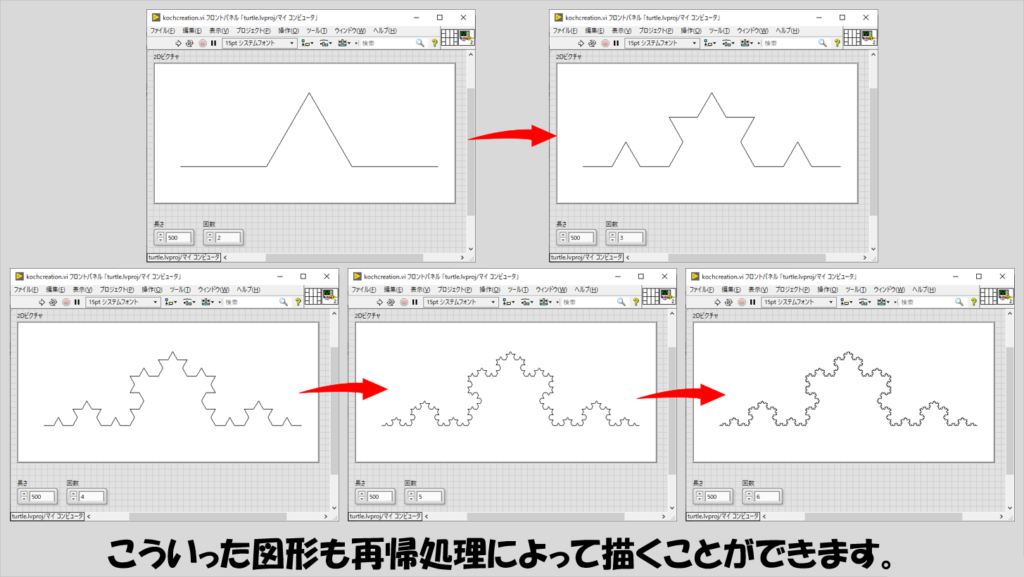
ある辺に三角形を書く、その三角形も一つ一つは「ある辺」とみなせるのでそこにも三角形を書く、ということが繰り返されています。
再帰処理の実装の仕方
再帰処理の組み方の基本と設定方法
ではLabVIEWで再帰処理を行うためにはどうすればいいか、ですが、再帰関数の本質は、「(ある処理を行う)関数自身の中でその関数を使う」ような構造にあります。
これを入れ子と呼んでいたわけですね。
そのために何が必要か?を一つずつ確認していきます。
まず、あるLabVIEWで「関数」とは(サブ)VIを指します。
そしてその中で、大まかに次の二つの状態が処理されうる、ということになります。
- 似た構造を持つ処理が実行される、入れ子になっている状態
- 入れ子になっていない状態
二つの状態は同じ瞬間に実行されることはなく、独立しているはずです(でなければ入れ子構造を必ず含む形となり永遠に処理が終わらない)。
独立した二つの状態を実行する、これは一つのVIで「場合分け」をすることに対応します。
場合分けといえばLabVIEWではケースストラクチャを使用しますが、ケースストラクチャを使用した場合、二つのケースを同時に実行することはできないので、今回の用途にぴったりです。
そこで、入れ子になっている状態となっていない状態とそれぞれのケースを作ります。
下の図のイメージですね。
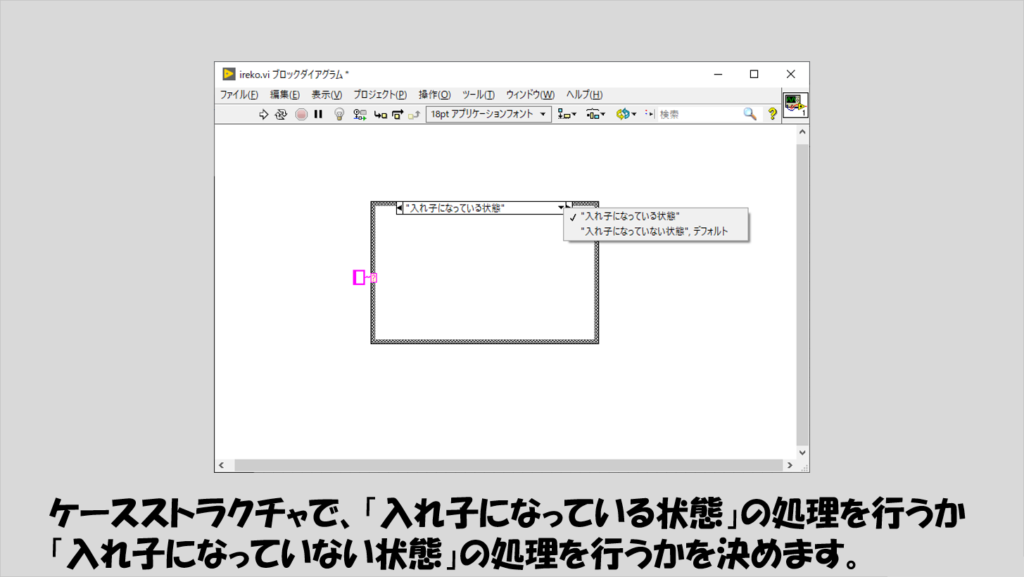
ここで注意するのは、「入れ子になっている状態」も「入れ子になっていない状態」も必ずしも1つ以上必要にはなりますが、「1つ」には限定せず何個もあっていい、ということです。
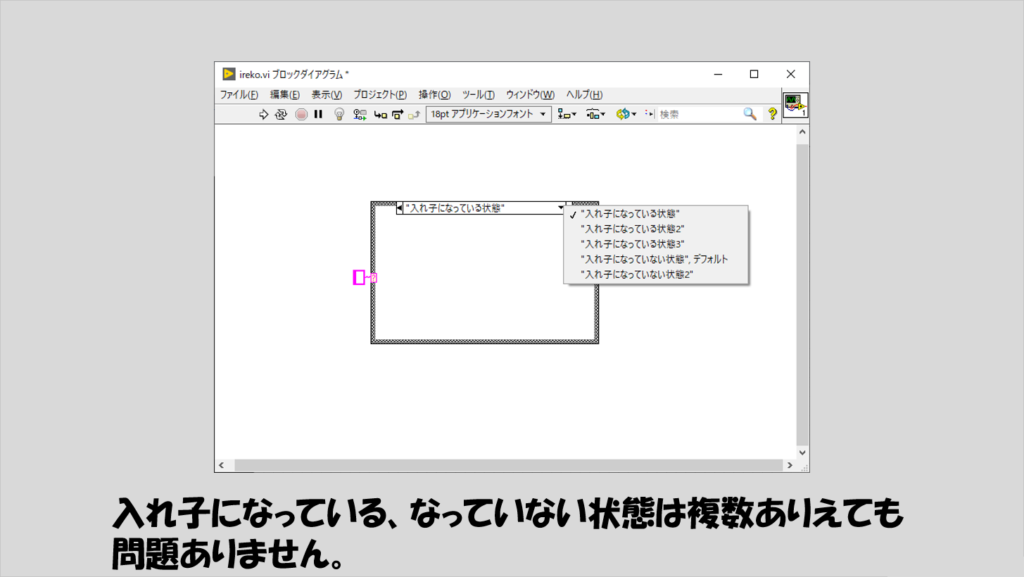
要は、入れ子になりうる処理は複数あってもいいし、それらの処理が行きつく先(入れ子になっていない状態)が複数あっても最終的にそのどれかに行きつきさえすれば不都合はないわけです。
あくまでイメージですが、以下のような感じです。この中で一つの状態だけが選ばれ、実行されます。
入れ子になっている状態となっていない状態とをケースストラクチャで用意出来たら、入れ子になっている状態に対して、文字通り「入れ子」にしてみます。
入れ子とは関数(=VI)自身の中でその関数を使うということだったので、何となくこんな形にしたらいいのではないか、ということで、VIのブロックダイアグラムに自分自身のアイコンを配置してみます。
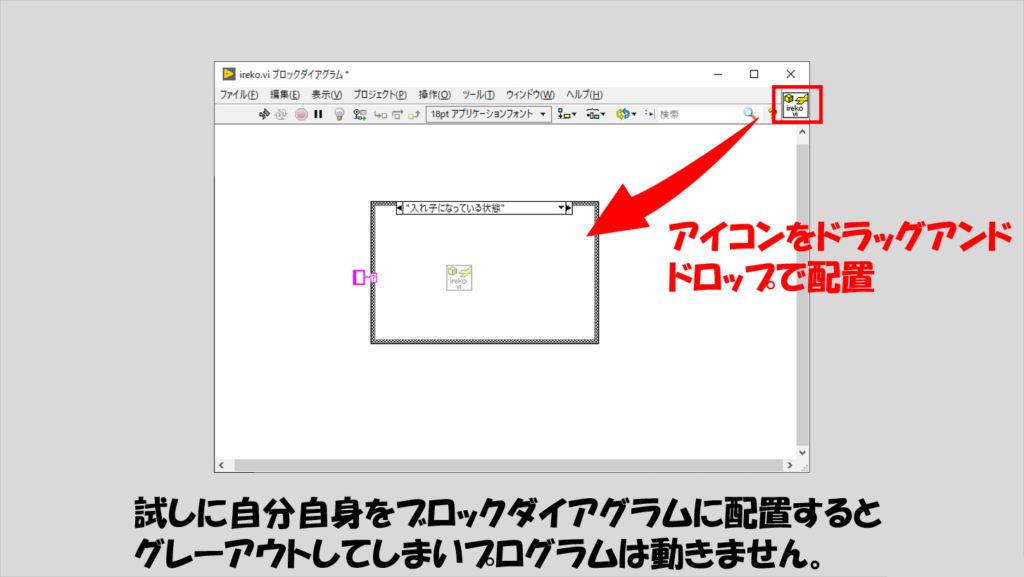
何となく配置してみましたが、グレーアウトしてうまくいかないですね。
これは、このサブVIに入出力がないからグレーアウトしているのではなく、設定自体がなされていないためグレーアウトしている状態です。
実は形としてはこれでいいのですが、VI自体の設定(VIプロパティ)をデフォルトの状態から変更する必要があります。
具体的には、クローン共有の形にする必要があります。
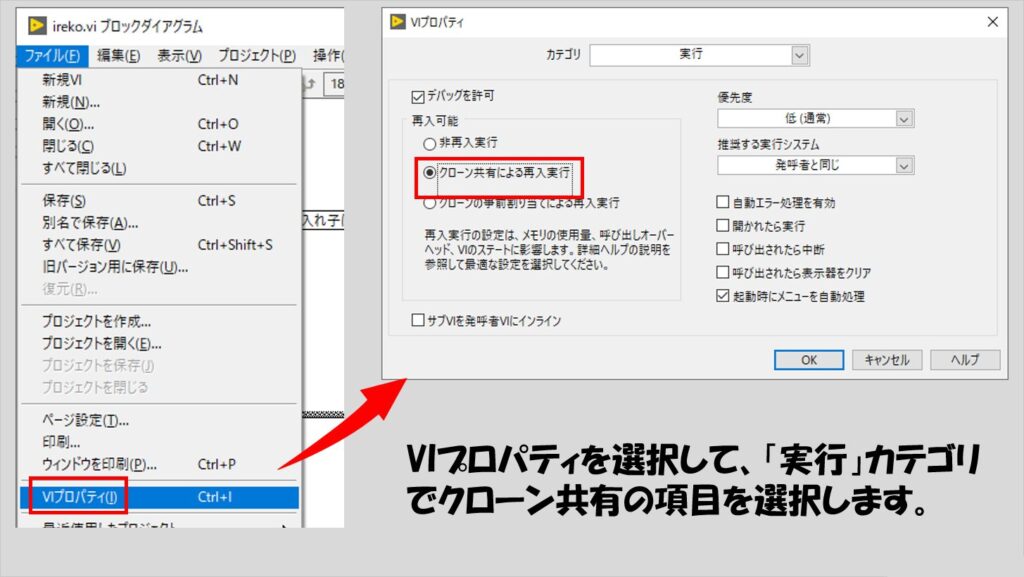
こうすることで、グレーアウトすることなく、自分自身をブロックダイアグラムに配置することができます。
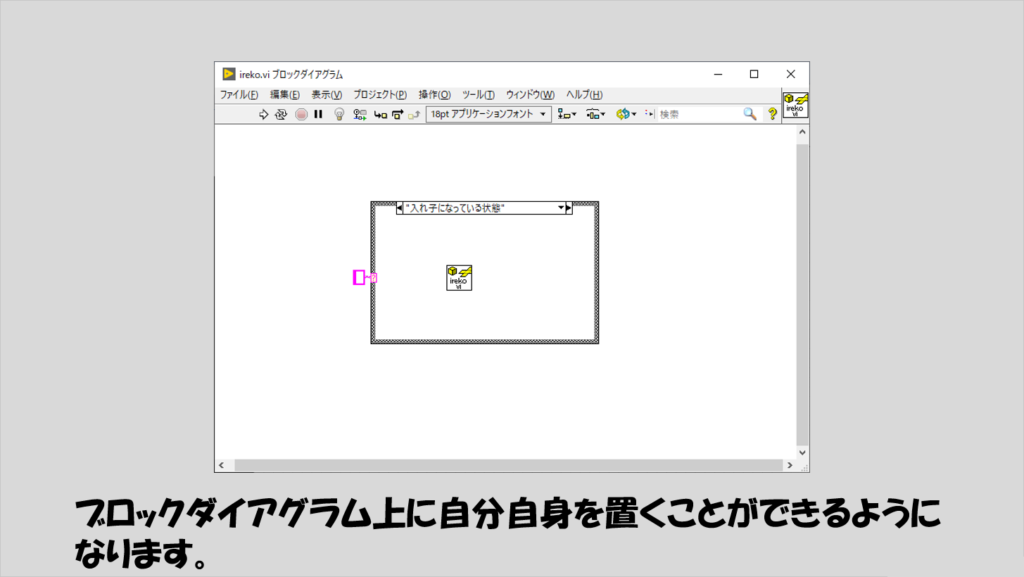
あと考えるべきは何か、といえば、「どのような条件で入れ子状態か入れ子じゃない状態を判断するか」ということですね。
つまり、ケースストラクチャの「?」の部分に配線する入力値は何にするか?を決める必要があります。
ここについては、何を再帰処理で扱うかによって様々あり得るので、具体的な例で見てみた方がわかりやすいと思います。
ということで、実際にLabVIEWで再帰的な処理を行う場合の例を2つ紹介します。
実践:フィボナッチ数列
まずは再帰処理の説明でも出てきたフィボナッチ数列についての再帰処理です。
指定したNのときのa_(N)を求めるような処理を実装するにはどうすればいいか?
早速具体的にフィボナッチ数列についての処理のLabVIEWでの実装例を示します。
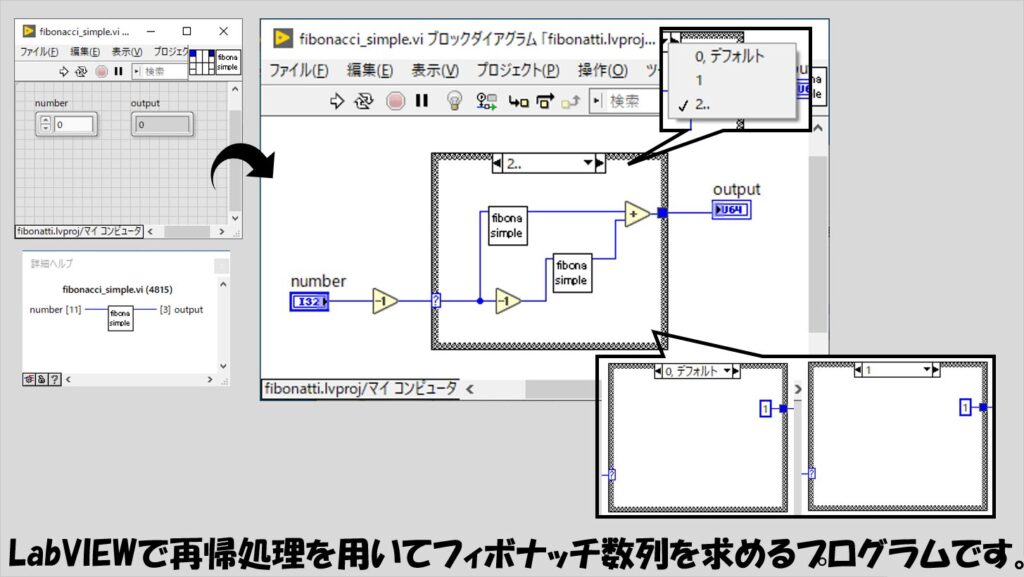
いきなり、入れ子になっている「2..」のケースにて自分自身を2つ置いている例となっていますが、何となくやっていることのイメージはできるでしょうか?
やっていることは、「a_(N)を求める」ことをそのまましているだけです。
なので、このVIに対して入力する必要があるのは「N」であり、得られる結果は「a_(N)」のはずです。
プログラム中では、「N」がnumber、「a_(N)」がoutput、としています。
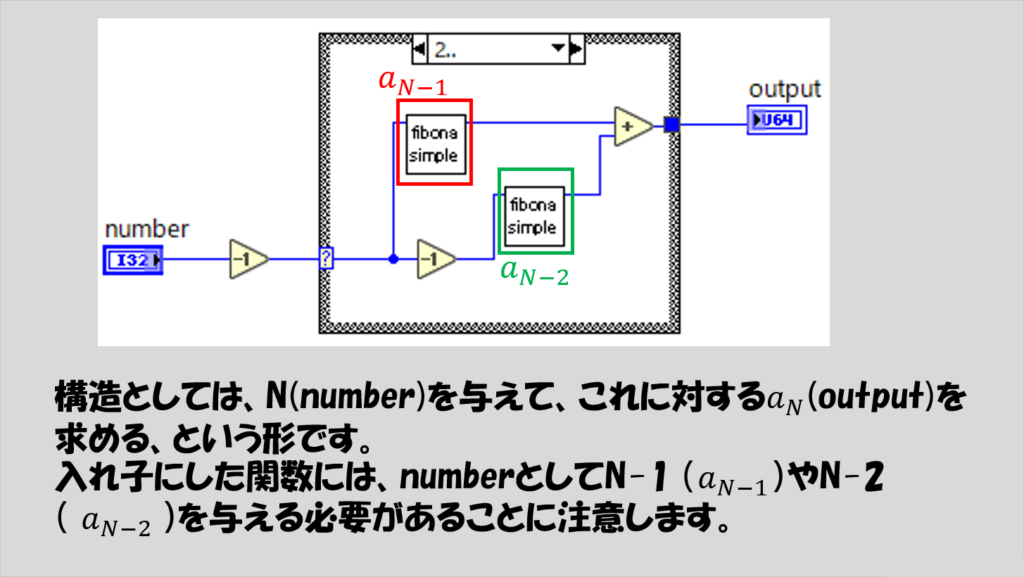
必要な入力として、a_(N)のNの部分にあたる数値(から1や2を引いた数)を入力値として入れ子にした関数に渡していることがわかるかと思います。
なお、上の実装では、ケースストラクチャの外でデクリメントを使用しているため、numberに対して渡す最小の数は1となります。
numberに1を指定した場合、ケースストラクチャの「0」のケースが実行されます。
注意:デクリメントするのがケースストラクチャの外でなければいけないわけではありません。ケースストラクチャの中に配置する場合でnumberを正の数に制限する場合には、「0」のケースは必要なくなり、「1」と「2」を独立させ、「3..」というケースを作ることになります。
試しにフィボナッチ数列のいくつかの要素を並べて書きだしてみます。
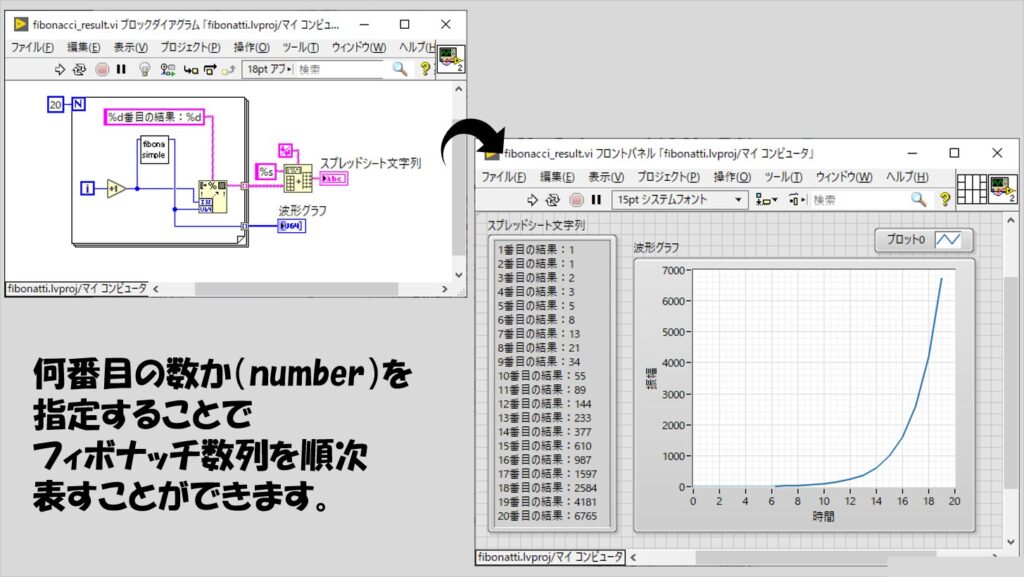
重要なのは、ケースストラクチャとして「0」と「1」のケースです。
これらのケースでは、自分自身を置いていません。入れ子じゃない状態、ですね。
なので、これらのケースが実行されたら、それ以上自分自身を実行することはなくなります。
このように、入れ子構造になっていたとしても最終的に行き着く先が入れ子構造を持たないような状態とし、処理が必ず入れ子構造になっていない状態にたどり着くようにする必要があります。
もしこの構造がわからないぞ、と思ったら、具体的な小さい数を入れて順を追って考えてみるとわかってくると思います。
実践:ファイル探索
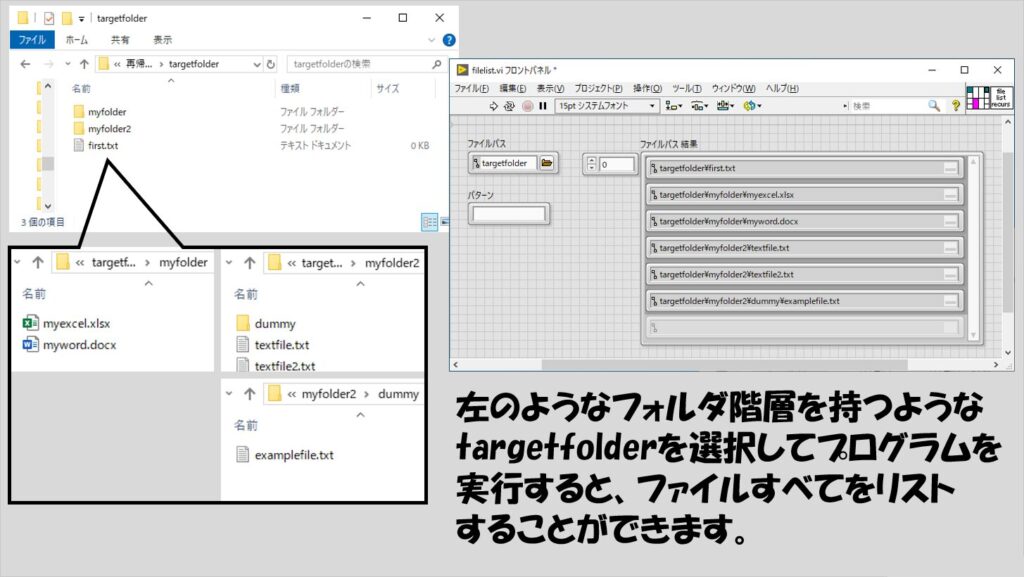
ではもう一つ別の例として特定のフォルダを指定したらそのフォルダの中にあるファイルを一覧としてリストするといった関数を作ることを考えます。
もしフォルダの中にファイル以外に別のフォルダがあった場合、そのフォルダの中身も調べてファイルがあるかどうかを見ます。
この、フォルダにまたフォルダが含まれていたらさらにそのフォルダも調べる・・・という、同じような処理を入れ子にして繰り返すので、再帰処理が使えます。
「あれ、LabVIEWに既にそんな機能を持つ関数がなかったっけ?」と知っている方からツッコミが入りそうですが、実はLabVIEWには標準関数として「再帰ファイルリスト」という関数があり、今から実装しようとしている処理をすることができます。
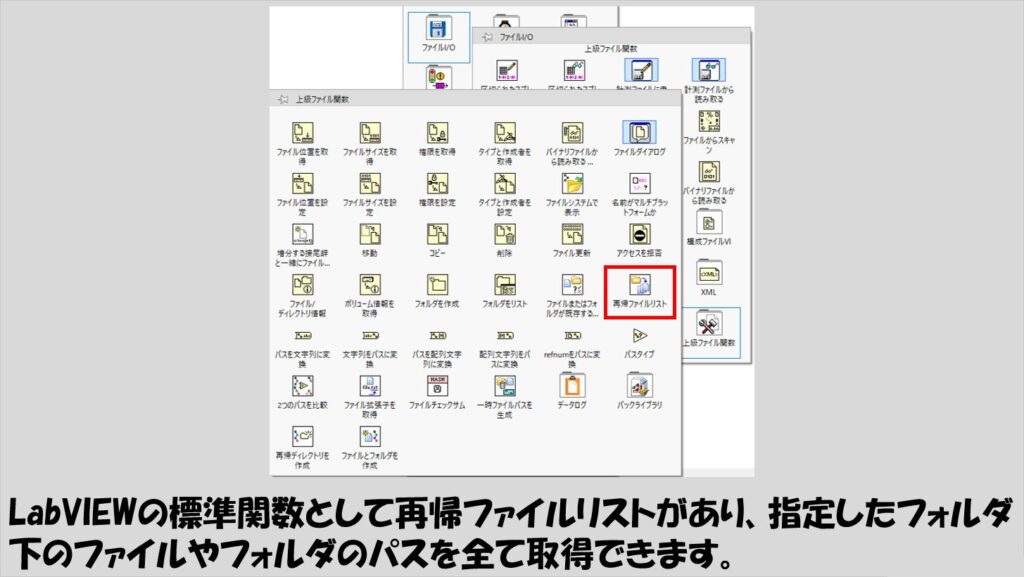
ただ、この「再帰ファイルリスト」の関数自体は、再帰のための設定(VIプロパティの設定)など行っておらず、中身もみても自分自身は使っていません。
処理の内容と結果を考えると確かに「再帰」なのですが、LabVIEWの再帰処理用の設定を用いた実装にはなっていない、ということですね。
そこで、再帰的な処理を実施した前提で実装例を以下に紹介します。
右側のケースストラクチャの「1..」の中で使用されているForループの出力トンネルのトンネルモードは「連結」になっていることに注意してください。
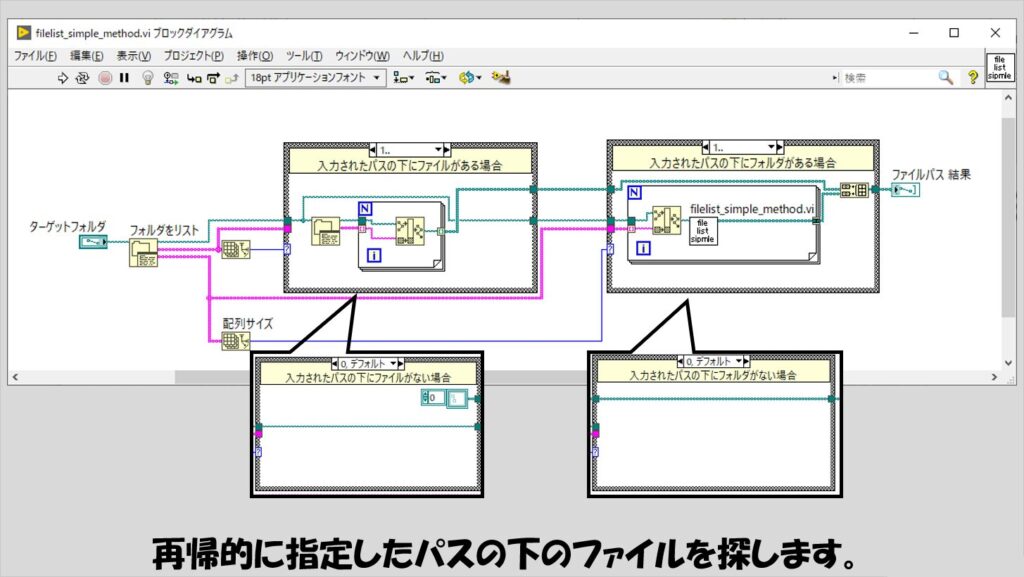
この例では、フィボナッチ数列の時同様に、数で場合分けをしていますが、その数は「指定したパスの下にフォルダやファイルが何個あるか」という情報になっています。
そして、入れ子になっているのは「入力されたパスの下にフォルダがある場合」のみでそれ以外は入れ子にならず処理を終了します。
これで目的の処理は達成することができます。
再帰処理実装の工夫
再帰処理を紹介する記事ではありますが、「再帰処理の設定をしないと再帰的な処理が実装できないわけではない」ということも覚えておくといいと思います。
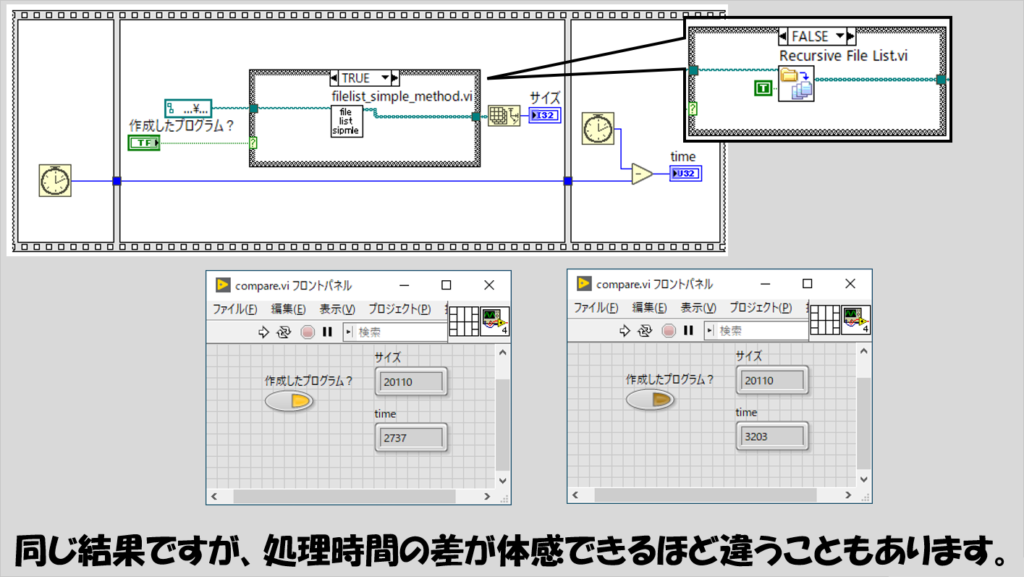
たとえば、すぐ上で紹介したファイルのリストを取得する再帰処理を例にとると、このプログラムと、LabVIEWの標準関数として存在する「再帰ファイルリスト」の関数とで、結果は同じになります。(再帰ファイルリストの関数の場合、「エラー時に再帰を継続?」のブール値がFalseになっていると全てのファイルを検索できない場合があります)
再帰ファイルリストは再帰処理の設定(VIプロパティにおいてクローン設定をして自分自身をブロックダイアグラムに配置)をしていなくても、実際再帰的な処理ができている、ということになりますね。
処理時間を比べると、異なる実装方法で有意に差が出ることもあります。
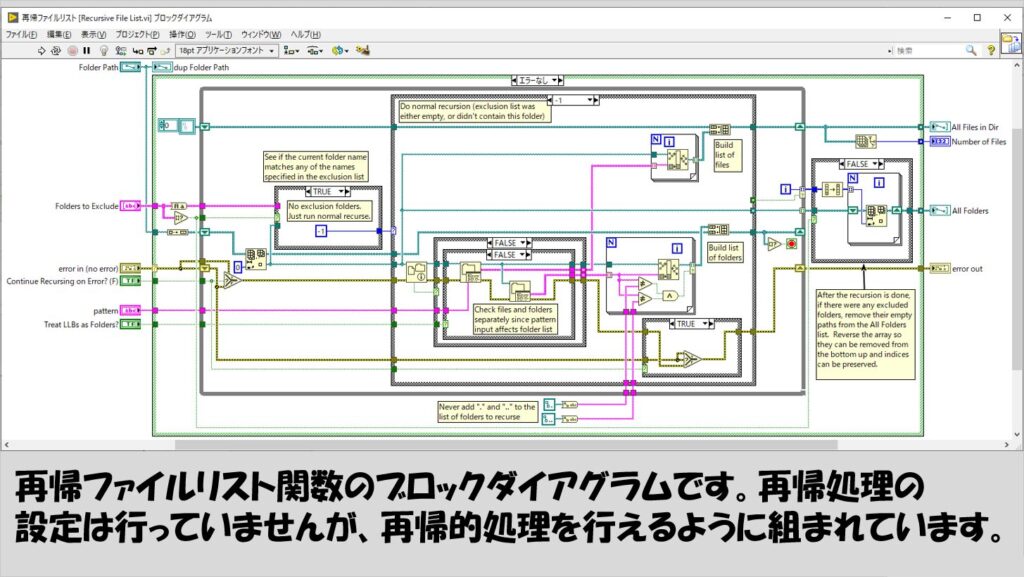
なお、再帰ファイルリストの関数をダブルクリックして中身を開くと、VI自体の再帰処理は行っていない代わりに、シフトレジスタを用いています。
シフトレジスタは、一つ前のループから処理を受け取ることができます。
これをうまく駆使すれば、再帰的な処理として入れ子状態にしなくても再帰処理を実装することができます。
どちらの方が実装が難しいか、は人それぞれだと思いますが、再帰の設定を行って、自分自身をブロックダイアグラム中で使用する書き方は慣れないととても混乱してしまうことがあるので、別のアプローチがとれないかを探るという選択肢も持っておくに越したことはない、と思います。
また、再帰処理を単に実行するだけでは処理に大きく時間がかかってしまうため、何かしらアルゴリズム的な工夫、改善を加えるといったことを考える必要がある場合もあります。
最初に紹介したフィボナッチ数列の計算のプログラムについても、Nを大きくした場合に処理にかなり時間がかかることがあります。
なぜ処理に時間がかかるかについては、「無駄な計算が多い」という理由が考えられます。
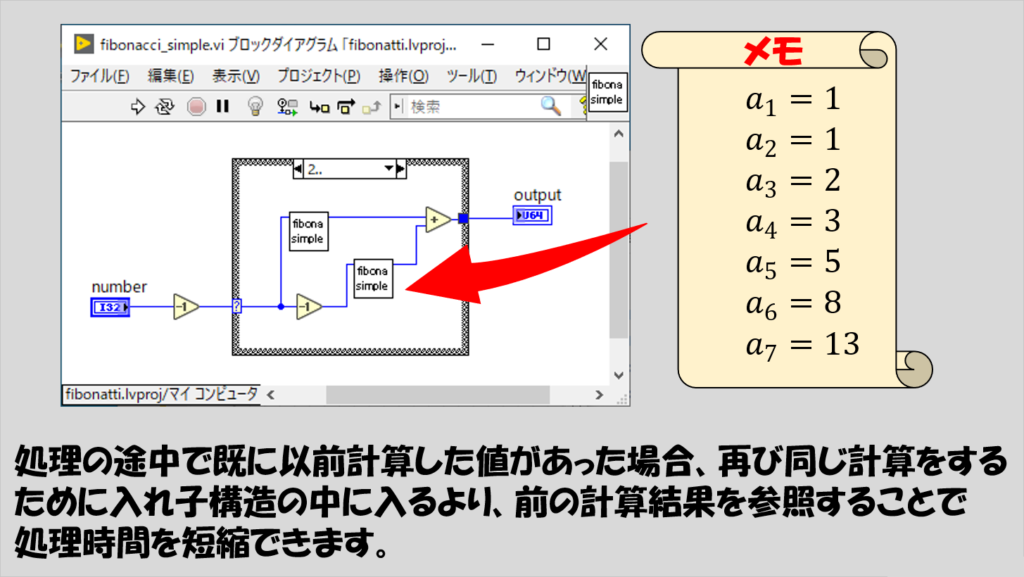
フィボナッチ数列の計算の場合、最終的にa_(1)とa_(2)の足し算に落とし込めることがわかります。
ということは、ここに行きつくまでに、同じ計算を何度も行っている部分があるはずです。
簡単な例としてa_(5)の計算を考えると、
a_(5) = a_(4) + a_(3)
となりますが、この前半の部分の計算a_(4)をするためにはa_(3)の値が必要となるためこの時点でa_(3)を計算しa_(3)=2という値を得ているはずです。
しかし、後半の部分の計算としてのa_(3)は、a_(4)の計算の時点でa_(3)=2という結果を得ているのはお構いなしに、a_(3) = a_(2) + a_(1)という計算を「無駄に」行ってしまいます。
もしそうではなく、プログラム自身が計算を行う過程で「a_(3) = 2だな」ということを覚えていれば、その後の計算でa_(3)の値が必要になったときに、いちいちa_(2) + a_(1)を計算することなく、a_(3) = 2という値を瞬時に使用して無駄を省くことができます。
実際Nの数が大きくなるとこのような無駄な処理の数は非常に多くなるため、この無駄を省くことができればその効果は絶大で、大幅な処理時間の短縮が見込めます。
他のプログラミング言語でもあるように、こうした再帰処理の無駄を効率よく処理するための方法として、動的メモ法があります。
今紹介したような「プログラム自身が計算を行う過程で「a_(3) = 2だな」ということを覚え」るように、既に計算した結果はメモとして残しておき瞬時にその値を活用する組み方です。
LabVIEWでもこの考え方を落としこんだプログラムを書くことができます。
フィボナッチ数列の場合には、例えば以下のような実装が考えらえます。
フロントパネル上には、メモの役割を果たすクラスタの配列を用意しておきます。
クラスタは、「N(number)のときのa_(N)(value)」というペアを示しています。
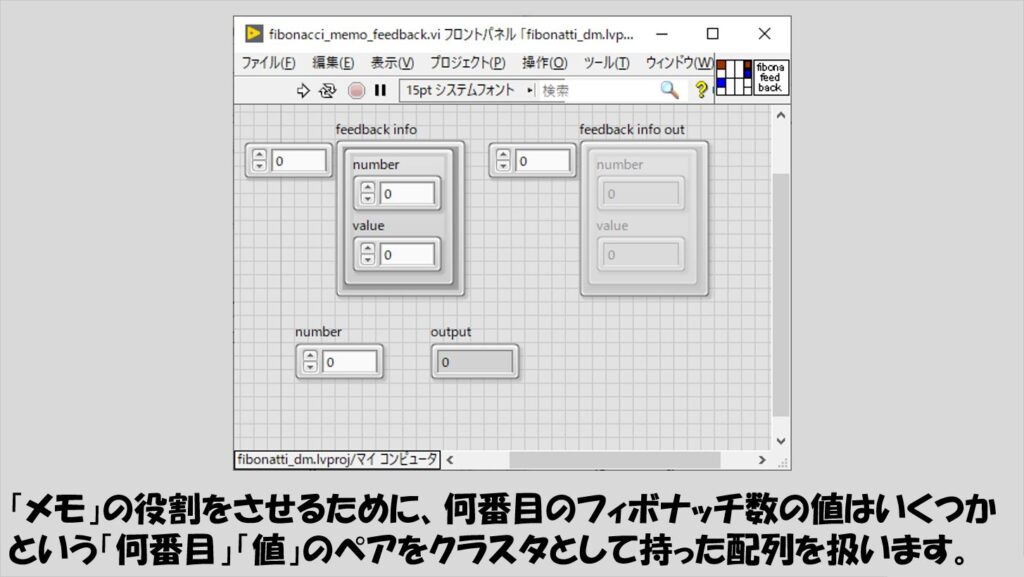
このメモを、フィードバックノードの初期化に使用することで、入れ子になっている関数にもメモの情報を渡す、という方針にしています。
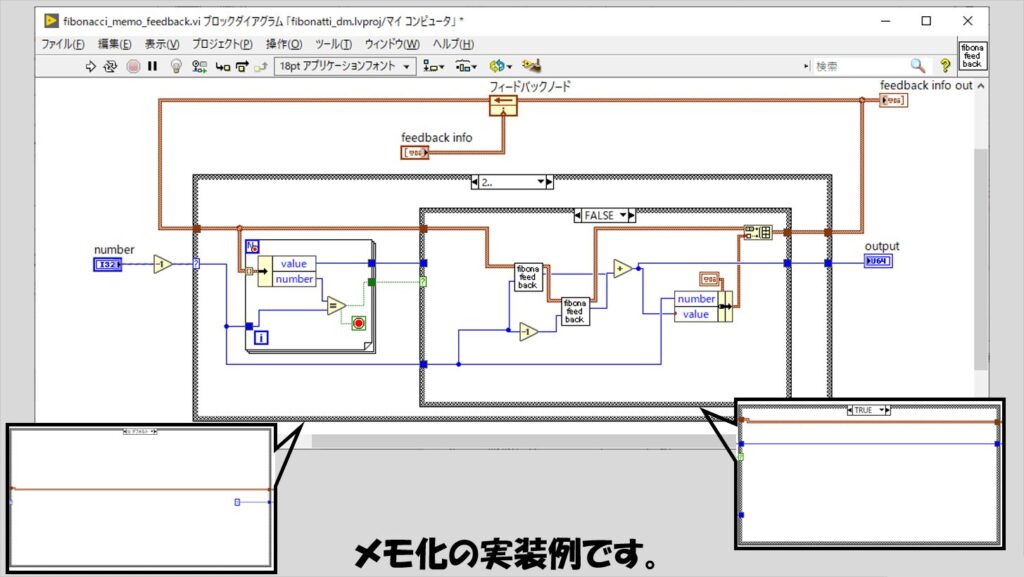
このフィードバックノードの方法以外に、グローバル変数を使用してメモを共有するという組み方も考えられると思います。
具体的には以下のような実装が考えられます。
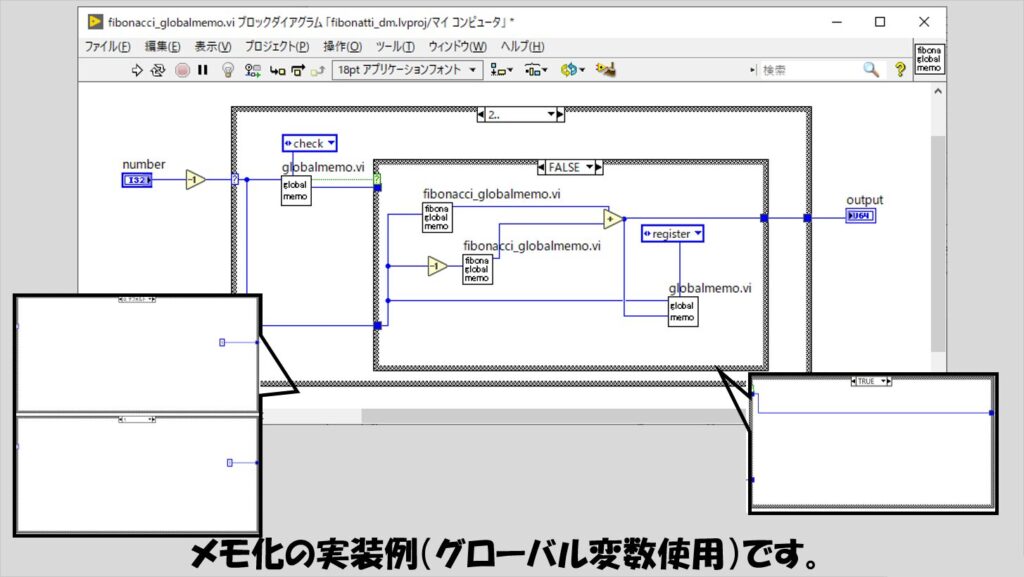
グローバル変数の役割を持つglobalmemo.viは以下のようにしておきます。(VIプロパティの設定では「非再入実行」としています)
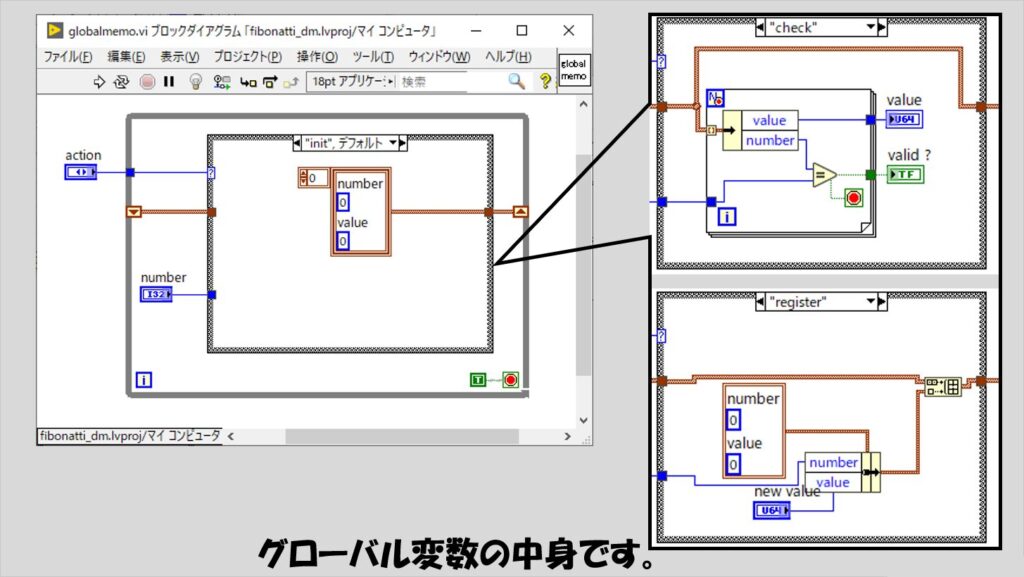
これらメモを使用した実装の方が、単なる再帰処理による処理よりも圧倒的に早く計算が終わります。
注記:フィードバックノードを使用した実装と、グローバル変数を使用した実装は等価であるかどうか私は判断が付けられていません。もしかしたらそもそもどちらかの実装の方が正しく、もう片方は場合によっては不正確な実装かもしれません。ただ、以下で示すように、どちらの方法であってもメモを使用しない場合よりは圧倒的に早く処理が終わります。
同じ結果が得られるのであれば、処理が早く終わるほうがいいのですが、工夫次第で処理時間が変わるということ自体知らなければこのような実装をしようともなかなか考えないかなと思います。
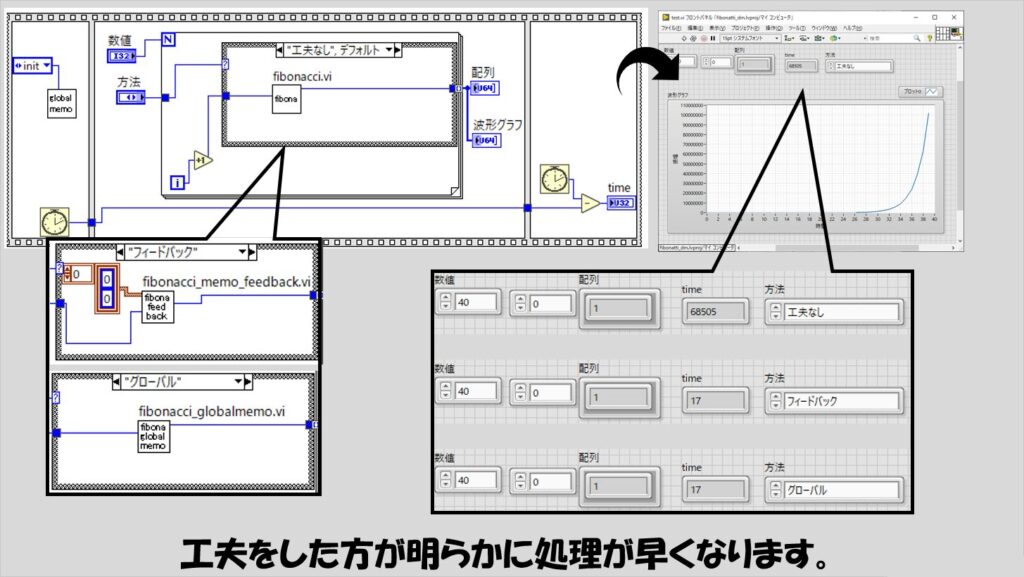
「再帰的な処理を行いたい」といった場合に、VIプロパティの設定を変更して単純に実装することで実現そのものはできるかもしれませんが、無駄が生じて結果的に処理終了に時間がかかってしまうということであれば、工夫をする必要がある(工夫をする余地がある)、ということを覚えておくといいと思います。
再帰処理に失敗している場合
最後に、再帰処理の設定をしたVIを実行していて、意図せず「入れ子の状態から抜け出せない」、つまり永遠と同じ処理をさまよってしまう場合にどうなるかについて紹介して終わります。
結論から言うと、LabVIEWがエラーメッセージを出します。
ただし、いわゆる関数のエラーとは異なるもので、メモリ不足のときのように、エラーのポップアップの設定をしていなくても表示されるランタイムエラーのようです。
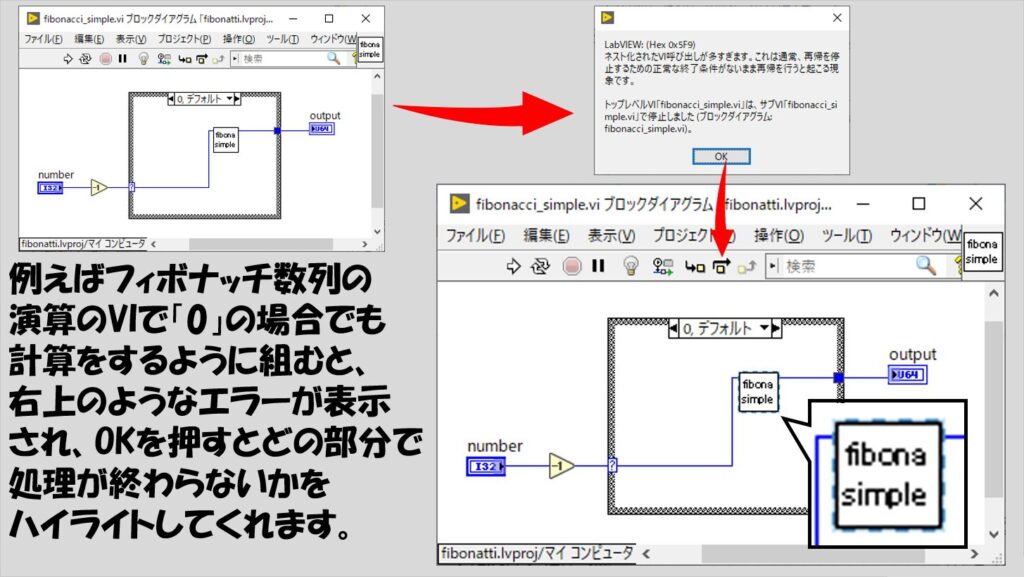
逆に、このエラーが出ないということは処理自体は進んでいるということで、プログラムの実行が終わらない場合には、組み方は合っているけれど単に再帰処理自体の処理が非常に多い、という判断ができそうです。
本記事では、LabVIEWで再帰処理を実行する方法と実装例を紹介しました。
再帰処理の書き方は慣れないとなかなか難しいと思いますが、再帰的な処理でしか実現できないような処理もあるので、まずは設定の仕方だけでもこの記事が参考になればうれしいです。
ここまで読んでいただきありがとうございました。
コメント